Diện tích đáy lớn của khối chóp cụt lục giác đều:
$[ S = \frac{3\sqrt{3}}{2} \cdot a^2 ]$
Thể tích của khối chóp cụt:
$[ V = \frac{1}{3} \cdot S \cdot h ]$
Diện tích đáy lớn của khối chóp cụt lục giác đều:
$[ S = \frac{3\sqrt{3}}{2} \cdot a^2 ]$
Thể tích của khối chóp cụt:
$[ V = \frac{1}{3} \cdot S \cdot h ]$
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA = SB = SC = SD = a\sqrt 2 \). Gọi \(I,J\) lần lượt là trung điểm của \(AB\) và \(C{\rm{D}}\).
a) Chứng minh \(AB \bot \left( {SIJ} \right)\).
b) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(SC\).
Cho hình hộp đứng \(ABCD.A'B'C'D'\) có cạnh bên \(AA' = 2a\) và đáy \(ABCD\) là hình thoi có \(AB = a\) và \(AC = a\sqrt 3 \).
a) Tính khoảng cách giữa hai đường thẳng \(B{\rm{D}}\) và \(AA'\).
b) Tính thể tích của khối hộp.
Cho hình chóp tứ giác đều \(S.ABCD\) có tất cả các cạnh đều bằng \(a\) và có \(O\) là giao điểm hai đường chéo của đáy.
a) Tính khoảng cách giữa hai đường thẳng \(AC\) và \(SB\).
b) Tinh thể tích của khối chóp.
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có \(AB = a\), góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \({60^ \circ }\).
a) Tính khoảng cách giữa hai đáy của hình lăng trụ.
b) Tinh thể tích của khối lăng trụ.
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\) có \(O\) là giao điểm của hai đường chéo, \(\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \). Tính khoảng cách từ \(O\) đến mặt phẳng \(\left( {SCD} \right)\).
Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình vuông cạnh \(a\). Cho biết \(SA = a\) và \(SA\) vuông góc với \(\left( {ABCD} \right)\).
a) Tính khoảng cách từ điểm \(B\) đến \(\left( {SAD} \right)\).
b) Tính khoảng cách từ điểm \(A\) đến cạnh \(SC\).
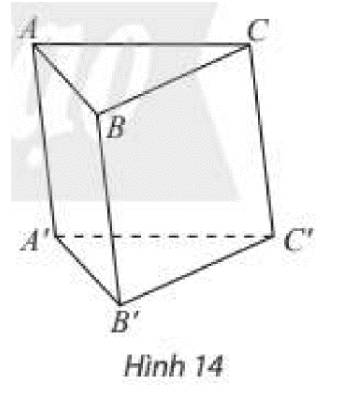
Cho khối lăng trụ tam giác \(ABC.A'B'C'\) (Hình 14). Tìm cách chia khối lăng trụ thành ba khối chóp có cùng chiều cao và diện tích đáy.
Cho hai tam giác cân \(ABC\) và \(ABD\) có đáy chung \(AB\) và không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng \(AB \bot CD\).
b) Xác định đoạn vuông góc chung của \(AB\) và \(C{\rm{D}}\).
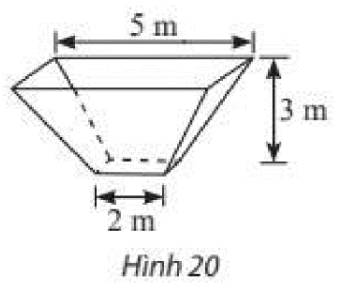
Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.