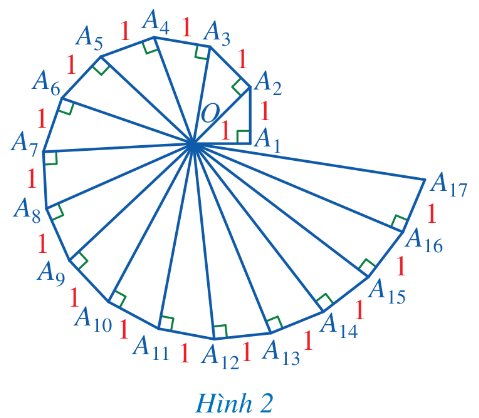
\(O{A_2} = \sqrt {1_{}^2 + 1_{}^2} = \sqrt 2 \).
\(OA_3^{} = \sqrt {\left( {\sqrt 2 } \right)_{}^2 + 1_{}^2} = \sqrt 3 \).
\(OA_4^{} = \sqrt {\left( {\sqrt 3 } \right)_{}^2 + 1_{}^2} = 2\).
\(OA_5^{} = \sqrt {2_{}^2 + 1_{}^2} = \sqrt 5 \).
=> \(OA_n^{} = \sqrt n \).
\(OA_6^{} = \sqrt 6 ,\) \(OA_7^{} = \sqrt 7 ,OA_8^{} = \sqrt 8 ,\) \(OA_9^{} = 3,\) \(OA_{10}^{} = \sqrt {10} ,\) \(OA_{11}^{} = \sqrt {11} ,OA_{12}^{} = \sqrt {12} ,\) \(\,OA_{13}^{} = \sqrt {13} \), \(OA_{14}^{} = \sqrt {14} ,\) \(OA_{15}^{} = \sqrt {15} ,\) \(OA_{16}^{} = 4,\) \(OA_{17}^{} = \sqrt {17} \).
Đúng 0
Bình luận (0)