Gọi các điểm như hình dưới:
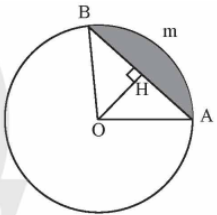
Gọi AmB là hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung có số đo $95^\circ$.
Vẽ $OH \perp AB$ tại $H$. Khi đó $H$ là trung điểm của $AB$.
Suy ra $AH = BH = \frac{AB}{2} = \frac{55}{2} = 27,5 \text{ (cm)}.$
Ta có $OA = OB = R$ nên $\Delta OAB$ cân tại $O$.
Mà $OH \perp AB$ nên $OH$ là tia phân giác của góc $AOB$, suy ra $\widehat {AOH} = \frac{\widehat {AOB}}{2} = \frac{95^\circ}{2} = 47,5^\circ.$
Áp dụng hệ thức giữa cạnh và góc trong $\Delta AOH$ vuông tại $H$, ta có:
$OH = AH \cdot \cot \widehat {AOH} = 27,5 \cdot \cot 47,5^\circ \approx 25,2 \text{ (cm)}; $
$OA = \frac{AH}{\sin \widehat {AOH}} = \frac{27,5}{\sin 47,5^\circ} \approx 37,3 \text{ (cm)}. $
Diện tích của tam giác $OAB$ là:
$S_{OAB} = \frac{1}{2} \cdot OH \cdot AB = \frac{1}{2} \cdot 25,2 \cdot 55 \approx 693 \text{ (cm}^2). \quad (1) $
Diện tích hình quạt tròn $OAmB$ là:
$S_{OAmB} = \frac{\pi R^2 n}{360} \approx \frac{\pi \cdot (37,3)^2 \cdot 95}{360} \approx 1153,42 \text{ (cm}^2). \quad (2) $
Từ $(1)$ và $(2)$ suy ra diện tích hình viên phân $AmB$ là:
$S_{AmB} = S_{OAmB} - S_{OAB} \approx 1153,42 - 693 \approx 460,42 \text{ (cm}^2). $



