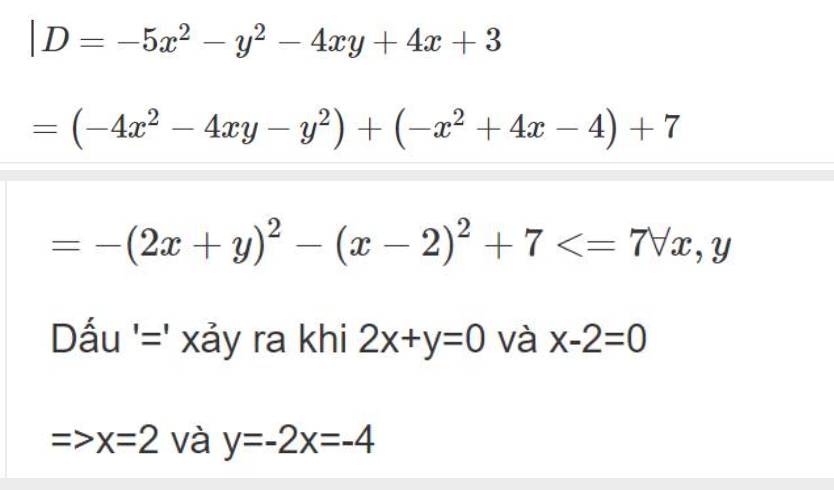
Vậy: \(D_{max}=7\) khi x=2 và y=-4
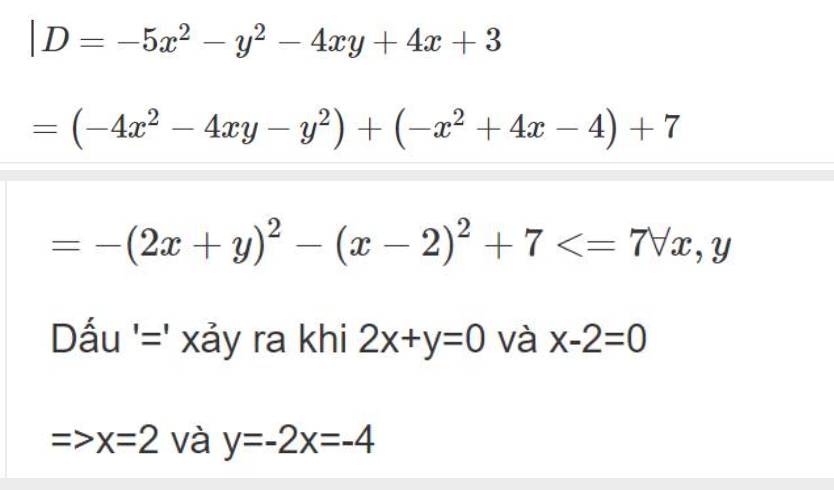
Vậy: \(D_{max}=7\) khi x=2 và y=-4
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
Tìm giá trị lớn nhất -2x^2-8x+1
-4xy+4x-y^2-5x^2+3 giúp chi tiết
Tính giá trị của biểu thức
a) x(x - 3xy ) - ( 4xy - 5x2 ) . \(\frac{3}{5}y\) với x = -2 và y = \(-\frac{1}{2}\)
b) ( y - 3x) 2x + ( 4y + \(\frac{3}{2}x\)) . 4x với x = -1 và y = \(\frac{1}{8}\)
1. Tìm GTLN của :
A = x^2 + 4x - 5
B = -2x^2 + 3x + 1
2. Tìm GTNN của :
a. x^2 + 4xy + 5y^2 - 2y + 3
b. x^2 + 10y^2 - 6xy - 2y + 6
c. 5x^2 + 7x + 4
d. x^2 - 5x - 2
Bài 1: Tính giá trị của biểu thức
\(\dfrac{3}{4}\) xy2(x2 + \(\dfrac{2}{3}\) xy + \(\dfrac{4}{3}\) y2) - \(\dfrac{1}{2}xy\) (-\(\dfrac{1}{2}x^2y\) + xy2 + y3) tại x = \(\dfrac{1}{2}\) , y = 2
Bài 2: Chứng minh đẳng thức
a) 5x(x2 + 2x - 1) - 3x2 ( x - 2) = x(2x2 - 1) + 4x(4x -1)
b) xy(2x3 - 3y3) - x2y2(5x + 4y) = 2x2y(x2 - xy + y2) - 3xy2(x2 + 2xy + y2)
c) 2y(x3 + x2y - \(\dfrac{1}{4}\) y3) - \(\dfrac{1}{2}\)x(2x3 + 4xy2 - y3) = \(\dfrac{1}{2}\)y3(x - y) - x3(x - 2y)
Bài 3: Tìm x thỏa mãn điều kiện
a) 6x(x - 4) + 2x(2 - 3x) = -25
b) 5x2(3x - 2) - 3x2(5x + 2) + 2x(3 + 8x) = 21
c) 5x(4x2 - 2x + 1) - 2x(10x2 - 5x - 2) = -36
tính:
1. -4x5(x3-4x2+7x-3)
2. 3x4(-2x3+5x2-\(\dfrac{2}{3}\)x+\(\dfrac{1}{3}\))
3. -5x2y4(3x2y3-2x3y2-xy)
4. 4x3y2(-2x2y+4x4-3y2)
TÌM X biết:
a. (5x - 2)(5x + 2) - (5x + 3)(5x - 4) = 8
b. (4x - 3)( 4x + 2) + (4x + 5)(1 - 4x) =2.52
1. Thực hiện phép tính
a. 4x^2.(5x^3-3x+1)
b. (5x^2-4x).(x-2)
c. (x^2-2xy+y^2).(x-y)
2. Phân tích các đa thức sau thành nhân tử
a. 2x^3 y-4x^2 y^2+2xy^3
b. x^2-y^2-3x-3y
3. Tìm x biết
a. 4x^2-4x=0
b. Tìm a để đa thức 2x^3-x^2+x+a chia hết cho đơn thức x-2
5x(4x^2-2x+1) -(2x(10x^2-5x-2) với x=3
x(x-y)+(x+y) với x=6 vào y=8
2x(3x^2-5x+8)-3x^2(2x-5) -16x với x=-15