Đặt \(a=\sqrt{2x-1}\left(a\ge0\right)\Rightarrow N=10-\dfrac{a^2+1}{2}+a\\ =10-\dfrac{a^2+1-2a}{2}\\ =10-\dfrac{\left(a-1\right)^2}{2}\le10\)
Vậy GTLN của N là \(10\) khi \(x=1\)
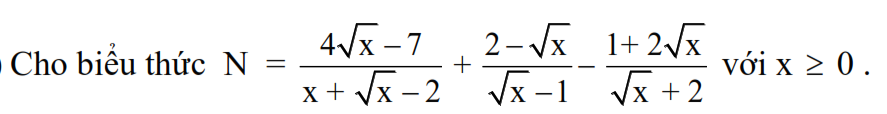
a) Tìm x để N=\(\dfrac{1}{2}\)
b) Tìm x ∈ \(Z\) sao cho N ∈ \(Z\)
c) Tìm GTLN của N
Tìm GTLN
x-\(\sqrt{x}+1\)
\(\dfrac{1}{\sqrt{x^2+2x+10}}\)
Cho biểu thức \(A=\left(\dfrac{2x+\sqrt{x}}{x\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{1+\sqrt{x}+x}\right)\left(\dfrac{x\sqrt{x}+1}{\sqrt{x}+1}-\sqrt{x}\right)\) với \(x\ge0;x\ne1\)
a) Rút gọn A
b) Tìm \(x\) để \(A-2x\) đạt GTLN
Tính GTLN của biểu thức B= \(1-\sqrt{x^2-2x+2}\)
Q = căn x )/(2 căn x +1) + (x+1)/(2x-căn x -1)*[(2x căn x -x- căn x)/(x căn x +1) - (x- căn x)/(x-1)]
rút gọn A tính gt của A khi x=7-4 căn3
tìm GTLN
Bài 1: tìm GTLN của A= (x+căn(x)+2)/(x-1)
Bài 1:
A=\(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
a) Tìm tập xác định của biểu thức A
b) Rút gọn biểu thức A
c) Chứng minh rằng A>0 với mọi x≠1
d) Tìm x để A đạt GTLN, tìm GTLN đó
Tìm GTLN của: \(A=\dfrac{\sqrt{x}+1}{2\sqrt{x}+1}\)
1. Tìm GTLN, NN của:
Q = \(\sqrt{x+1}+\sqrt{3-x}-2\sqrt{\left(x+1\right)\left(3-x\right)}\)
2. Tìm x,y thuộc N:
\(\frac{11x}{5}-\sqrt{2x+1}=3y-\sqrt{4y-1}+2\)
