a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = 6{x^2} + 6x - 36\).
Nhận xét \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 3\end{array} \right.\).
Ta có bảng biến thiên sau:

Vậy hàm số đạt cực đại tại điểm \(x = - 3\) và đạt cực tiểu tại \(x = 2\).
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y' = -{4x^3} - 4x\).
Nhận xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên sau:
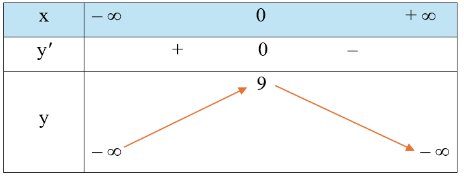
Vậy hàm số đạt cực tiểu tại \(x = 0\).
c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Ta có: \(y' = 1 - \frac{1}{{{x^2}}}\).
Nhận xét: \(y' = 0 \Leftrightarrow 1 - \frac{1}{{{x^2}}} = 0 \Leftrightarrow x = \pm 1\).
Ta có bảng biến thiên sau:
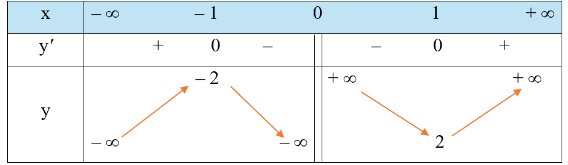
Vậy hàm số đạt cực đại tại x = -1 và đạt cực tiểu tại x = 1.


