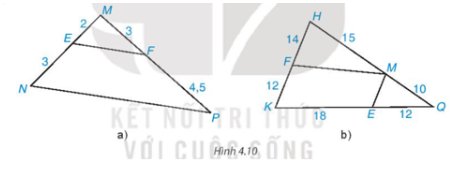
• Hình 4.10a)
Ta có: \(\dfrac{{EM}}{{EN}} = \dfrac{2}{3};\dfrac{{MF}}{{PF}} = \dfrac{3}{{4,5}} = \dfrac{2}{3}\) nên \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\)
Vì \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\), E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // MN.
• Hình 4.10b)
* Ta có: \(\dfrac{{HF}}{{KF}} = \dfrac{{14}}{{12}} = \dfrac{7}{6};\dfrac{{HM}}{{MQ}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\)
Vì \(\dfrac{{HF}}{{KF}} \ne \dfrac{{HM}}{{MQ}}\) nên MF không song song với KQ.
* Ta có: \(\dfrac{{MQ}}{{MH}} = \dfrac{{10}}{{15}} = \dfrac{2}{3};\dfrac{{EQ}}{{EK}} = \dfrac{{12}}{{18}} = \dfrac{2}{3}\)
Vì \(\dfrac{{MQ}}{{MH}} = \dfrac{{EQ}}{{EK}}\); F ∈ HK; M ∈ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.