\(\int_1^2\sqrt{1+x}dx=\int_1^2\sqrt{1+x}d(1+x)=\dfrac{2}{3}(1+x)^{3/2}|_1^2=...\)
cho mình mấy cái like , mình sẽ like lại hco mọi người ![]()
Dat \(\sqrt{x+1}\)=t ->x->dx
Doi can roi lam nhu binh thuong ban nhe
\(\int_1^2\sqrt{1+x}dx=\int_1^2\sqrt{1+x}d(1+x)=\dfrac{2}{3}(1+x)^{3/2}|_1^2=...\)
cho mình mấy cái like , mình sẽ like lại hco mọi người ![]()
Dat \(\sqrt{x+1}\)=t ->x->dx
Doi can roi lam nhu binh thuong ban nhe
Tính các tích phân sau:
a) \(\int_0^1x^3\sqrt{1-x^2}dx\)
b) \(\int_1^2\dfrac{dx}{x^2-2x+2}\)
c) \(\int_1^2\dfrac{dx}{\sqrt{4-x^2}}\)
d) \(\int_0^1x\sqrt{x^2+1}dx\)
\(\int_0^1\left|x^4-\left(-x+2\right)^2\right|dx\)
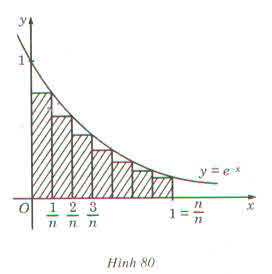
Một hình phẳng được giới hạn bởi \(y=e^{-x};y=0;x=0;x=1\)
Ta chia đoạn \(\left[0;1\right]\) thành n phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như hình 80)
a) Tính diện tích \(S_n\) của hình bậc thang (tổng diện tích của n hình chữ nhật con)
b) Tìm \(\lim\limits_{n\rightarrow\infty}S_n\) và so sánh với cách tính diện tích hình phẳng này bằng công thức tính tích phân
\(\int_0^1\left|\left(y^2\right)^2-\left(-y+2\right)^2\right|dx\)
\(\int_0^1\left|\left(e^Y\right)^2\right|dx\)
Tính diện tích hình phẳng giới hạn bởi các đường sau :
a) \(y=2x-x^2;x+y=2\)
b) \(y=x^3-12x;y=x^2\)
c) \(x+y=1;x+y=-1;x-y=1;x-y=-1\)
d) \(y=\dfrac{1}{1+x^2};y=\dfrac{1}{2}\)
e) \(y=x^3-1\) và tiếp tuyến với \(y=x^3-1\) tại điểm \(\left(-1;-2\right)\)
\(\int_1^e\left|\left(x.Lnx\right)^2\right|dx\)
Diện tích hình phẳng giới hạn bởi đường thẳng y=x+3 , đường cong y=x^2+1 là
Tính diện tích hình phẳng giới hạn bởi các đường :
a) \(y=x^2;y=x+2\)
b) \(y=\left|\ln x\right|;y=1\)
c) \(y=\left(x-6\right)^2;y=6x-x^2\)