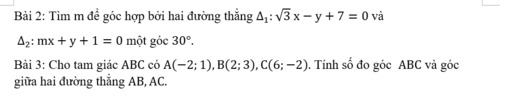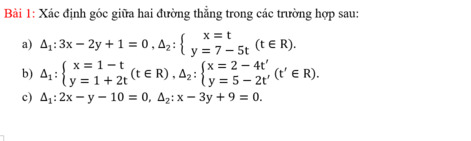Question

thank u

Answer 1

\(AB=\sqrt{\left(2+2\right)^2+\left(3-1\right)^2}=\sqrt{4^2+2^2}=2\sqrt{5}.\)

\(BC=\sqrt{\left(6-2\right)^2+\left(-2-3\right)^2}=\sqrt{4^2+\left(-5\right)^2}=\sqrt{41}.\)

\(AC=\sqrt{\left(6+2\right)^2+\left(-2-1\right)^2}=\sqrt{8^2+\left(-3\right)^2}=\sqrt{73}.\)

Xét \(\Delta ABC:\)

Áp dụng định lý cosin ta có:

\(\cos\widehat{ABC}=\dfrac{BC^2+AB^2-AC^2}{2BC.AB}=\dfrac{41+20-73}{2.2\sqrt{205}}\approx0,21.\\\Rightarrow \widehat{ABC}\approx102,09^o.\)