Lời giải:
Lấy điểm $M$ trên $BC$ sao cho $\widehat{MAC}=60^0$
Tam giác $AMC$ có góc $\widehat{C}=\widehat{A}=60^0$ nên $AMC$ là tam giác đều
$\Rightarrow AM=MC=AC=20$
Mặt khác:
$\widehat{MBA}=90^0-\widehat{C}=90^0-60^0=30^0$
$\widehat{MAB}=\widehat{BAC}-\widehat{MAC}=90^0-60^0=30^0$
$\Rightarrow \widehat{MBA}=\widehat{MAB}$ nên tam giác $MAB$ cân tại $M$
$\Rightarrow MB=MA=20$
Do đó:
$BC=MB+MC=20+20=40$ (cm)
Áp dụng định lý Pitago: $AB=\sqrt{BC^2-AC^2}=\sqrt{40^2-20^2}=20\sqrt{3}$ (cm)
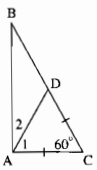
+ Vì \(\Delta ABC\) vuông tại \(A\left(gt\right)\)
=> \(\widehat{B}+\widehat{C}=90^0\) (tính chất tam giác vuông).
=> \(\widehat{B}+60^0=90^0\)
=> \(\widehat{B}=90^0-60^0\)
=> \(\widehat{B}=30^0.\)
Mà \(\widehat{C}=60^0\left(gt\right)\)
=> \(\Delta ACD\) là tam giác đều.
Mà \(\widehat{B}=30^0\left(cmt\right)\)
=> \(AC=CD=DB.\)
Mà \(AC=20cm\left(gt\right)\)
=> \(AC=CD=DB=20\left(cm\right).\)
Ta có: \(BC=CD+DB\)
=> \(BC=20+20\)
=> \(BC=40\left(cm\right).\)
+ Xét \(\Delta ABC\) vuông tại \(A\left(gt\right)\) có:
\(AB^2+AC^2=BC^2\) (định lí Py - ta - go).
=> \(AB^2+20^2=40^2\)
=> \(AB^2+400=1600\)
=> \(AB^2=1600-400\)
=> \(AB^2=1200\)
=> \(AB=\sqrt{1200}\)
=> \(AB=20\sqrt{3}\left(cm\right)\) (vì \(AB>0\)).
Vậy \(AB=20\sqrt{3}\left(cm\right);BC=40\left(cm\right).\)
Chúc bạn học tốt!
áp dụng tỉ số lượng giác trong tam giác ABC vuông, ta có:
\(\tan C=\frac{AB}{AC}\)
<-> tan 60 = \(\frac{AB}{20}\)
<->AB = \(\frac{tan60}{20}\)
<-> AB= 20 √3
áp dụng định lí pi-ta- go trong tam giác vuông ABC, ta có:
AB2 + AC2 = BC2
thay số: 1200 + 400= BC2
<-> BC 2= 1600
<-> BC =40















