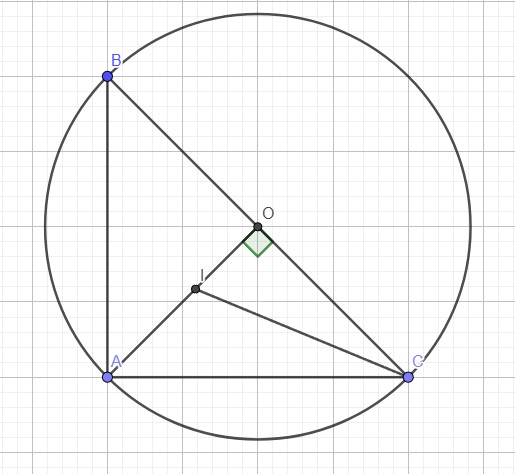
Tam giác ABC vuông cân tại A nên O đồng thời là trung điểm BC
\(\Rightarrow OA=OB=OC=R\)
Và \(AO\) là phân giác góc A
Kẻ phân giác góc C cắt AO tại I \(\Rightarrow I\) là tâm đường tròn nội tiếp tam giác ABC
\(AO\perp BC\Rightarrow IO\perp BC\Rightarrow IO=r\)
Do ABC vuông cân tại A \(\Rightarrow BC=AC\sqrt{2}\Rightarrow2OC=AC\sqrt{2}\Rightarrow\dfrac{OC}{AC}=\dfrac{1}{\sqrt{2}}\)
Áp dụng định lý phân giác:
\(\dfrac{OI}{AI}=\dfrac{OC}{AC}=\dfrac{1}{\sqrt{2}}\Rightarrow OI\sqrt{2}=AI=OA-OI\)
\(\Rightarrow\left(1+\sqrt{2}\right)OI=OA\)
\(\Rightarrow\left(1+\sqrt{2}\right)r=R\)
\(\Rightarrow\dfrac{R}{r}=1+\sqrt{2}\Rightarrow\left\{{}\begin{matrix}a=b=1\\c=2\end{matrix}\right.\)