ta có: 1+\(\dfrac{-99}{100}=1-\dfrac{99}{100}=\dfrac{1}{100}\)
\(1+\dfrac{-100}{101}=1-\dfrac{100}{101}=\dfrac{1}{101}\)
Nhận thấy \(\dfrac{1}{100}>\dfrac{1}{101}\) \(\Rightarrow x>y\)
Phân tích ra số thập phân nhé bạn, hoặc là lấy x - y:
+ Nếu ra kết quả là số dương thì x > y.
+ Nếu ra kết quả là số âm thì x < y.
Giải:
Ta có:
\(x=-\dfrac{99}{100}\)
\(y=-\dfrac{100}{101}\)
Vì \(-\dfrac{99}{100}-\left(-\dfrac{100}{101}\right)=-\dfrac{1}{10100}\)
=> \(x< y\)
ta có x=\(\dfrac{-99\cdot-101}{100\cdot-101}\) ; y=\(\dfrac{100\cdot100}{100\cdot-101}\)
=> x=\(\dfrac{-\left(99\cdot101\right)}{-\left(100\cdot101\right)}\)=\(\dfrac{99\cdot101}{100\cdot101}\)> hoặc = 0
y=\(\dfrac{100\cdot100}{-\left(100\cdot101\right)}\)< 0
x> hoặc = 0 > y
=> x>y
(dương thì lớn hơn âm )![]()
Cách nhanh nè , nhớ tích mình vs nhá
\(1+x=1+\left(-\dfrac{99}{100}\right)=\dfrac{1}{100}\)
\(1+y=1+\left(-\dfrac{100}{101}\right)=\dfrac{1}{101}\)
Vì \(\dfrac{1}{100}>\dfrac{1}{101}\) nên 1+x > 1+y do đó x>y









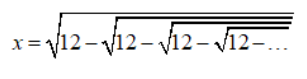 thì x bằng bn
thì x bằng bn





