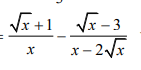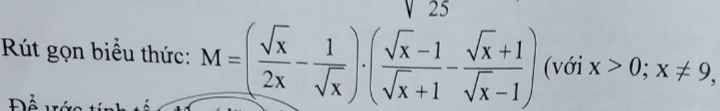Question

rút gọn giúp em ạ

Answer 1

ĐKXĐ :   \(\left\{{}\begin{matrix}x>0\\x\ne4\end{matrix}\right.\)

Có :  \(\dfrac{\sqrt{x}+1}{x}-\dfrac{\sqrt{x}-3}{x-2\sqrt{x}}\)

=  \(\dfrac{\sqrt{x}+1}{x}-\dfrac{\left(\sqrt{x}-3\right)\left(x+2\sqrt{x}\right)}{\left(x-2\sqrt{x}\right)\left(x+2\sqrt{x}\right)}\)

=  \(\dfrac{\sqrt{x}+1}{x}-\dfrac{x\sqrt{x}+2x-3x-6\sqrt{x}}{x^2-4x}\)

=  \(\dfrac{\left(\sqrt{x}+1\right)\left(x-4\right)}{x\left(x-4\right)}-\dfrac{x\sqrt{x}-x-6\sqrt{x}}{x\left(x-4\right)}\)

=  \(\dfrac{x\sqrt{x}-4\sqrt{x}+x-4-x\sqrt{x}+x+6\sqrt{x}}{x\left(x-4\right)}\)

=  \(\dfrac{2x+2\sqrt{x}-4}{x\left(x-4\right)}\)

=  \(\dfrac{2\left(x+\sqrt{x}-2\right)}{x\left(x-4\right)}\)

=  \(\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{x\left(x-4\right)}\)

mik rút gọn đc đến đây thôi, nếu có j nhầm lẫn thì bn thông cảm