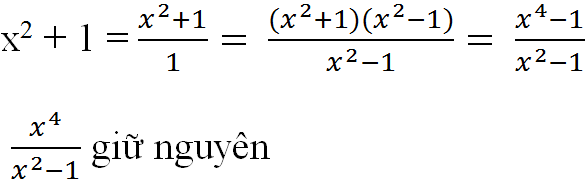Bài giải
a) \(\dfrac{1}{x+2}=\dfrac{x.\left(x-2\right)}{\left(x+2\right)\left(x-2\right).x}=\dfrac{x^2-2x}{x\left(x+2\right)\left(x-2\right)}\)
\(\dfrac{8}{2x-x^2}=\dfrac{8}{x\left(2-x\right)}=-\dfrac{8}{x\left(x-2\right)}=-\dfrac{8.\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}\)
b) \(x^2+1=\dfrac{x^2+1}{1}=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x^2-1}=\dfrac{x^4-1}{x^2-1}\)
\(\dfrac{x^4}{x^2-1}\) giữ nguyên.
c) \(\dfrac{x^3}{x^3-3x^2y+3xy^2-y^3}=\dfrac{x^3}{\left(x-y\right)^3}=\dfrac{x^3.y}{\left(x-y\right)^3.y}=\dfrac{x^3y}{y\left(x-y\right)^3}\)
\(\dfrac{x}{y^2-xy}=\dfrac{x}{y.\left(y-x\right)}=-\dfrac{x}{y.\left(x-y\right)}=-\dfrac{x\left(x-y\right)^2}{y.\left(x-y\right).\left(x-y\right)^2}=\dfrac{x\left(x-y\right)^2}{y.\left(x-y\right)^3}\)
*Phân tích thành nhân tử:
x+2
2x-x2=x(2-x)
*MTC:x(2-x)(x+2)
*NTP:x(2-x);x+2
*Quy đồng
\(\dfrac{1}{x+2}\)=\(\dfrac{1x\left(2-x\right)}{\left(x+2\right)x\left(2-x\right)}=\dfrac{1x\left(2-x\right)}{x\left(2-x\right)\left(x+2\right)}\)
\(\dfrac{8}{x\left(2-x\right)}\)\(\dfrac{8\left(x+2\right)}{x\left(2-x\right)\left(x+2\right)}\)=\(\dfrac{8x+16}{x\left(2-x\right)\left(x+2\right)}\)