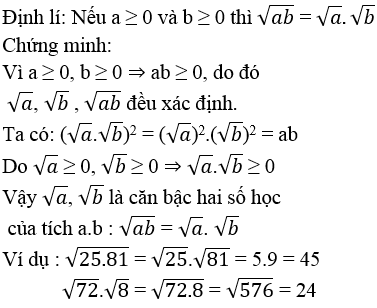Ôn tập chương 1: Căn bậc hai. Căn bậc ba
Các câu hỏi tương tự
Phát biểu và chứng minh định lí về mối liên hệ giữa phép chia và phép khai phương. Cho ví dụ ?
ĐỀ 1Bài 1: (3,0 điểm) 1. Thực hiện các phép tính: a) 2. Không dùng máy tính và bảng số hãy so sánh: 5 và Bài 2: (3,0 điểm) Rút gọn các biểu thức sau: a) b) c) Bài 3: (3,5 điểm) Cho biểu thức với x ³ 0 và x ¹ 1. a) Chứng minh: b) Tính giá trị của A khi c) Tìm các giá trị của x sao cho Bài 4: (0,5 điểm)Tìm giá trị nhỏ nhất của biểu thức:B với x 2017
Đọc tiếp
ĐỀ 1
Bài 1: (3,0 điểm)
1. Thực hiện các phép tính:
a) ![]()
![]()
2. Không dùng máy tính và bảng số hãy so sánh: 5 và ![]()
Bài 2: (3,0 điểm) Rút gọn các biểu thức sau:
a) ![]()
b) ![]()
c) 
Bài 3: (3,5 điểm)
Cho biểu thức  với x ³ 0 và x ¹ 1.
với x ³ 0 và x ¹ 1.
a) Chứng minh: 
b) Tính giá trị của A khi ![]()
c) Tìm các giá trị của x sao cho 
Bài 4: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức:
B =  với x > 2017
với x > 2017
Nêu điều kiện để \(x\) là căn bậc hai số học của số a không âm. Cho ví dụ ?
a) Chứng minh :
\(x-4\sqrt{x-4}=\left(\sqrt{x-4}-2\right)^2\)
b) Tìm điều kiện xác định và rút gọn biểu thức :
\(A=\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}\)
1. Cho biểu thức:
A= \((\dfrac{1}{x-\sqrt{x}} + \dfrac{1}{\sqrt{x}-1}) : \dfrac{\sqrt{x}-1}{x-2\sqrt{x}+1}\)
a) Tìm điều kiện xác định và rút gọn biểu thức
b) Tìm x để A> -1
c) Chứng minh với mọi x thuộc điều kiện xác định thì A<1
Làm giúp mình câu c với ạ!!
Cho biểu thức B=1+1/1căn 2+1/căn 3+...+1/căn 2010. Chứng minh rằng B>86
Với mỗi số nguyên dương n, đặt s_{n} (2 - sqrt{3})^n + (2 + sqrt{3})^na) Chứng minh rằng: s_{n+2} 4s_{n+1} - s_{n}b) Chứng minh rằng sn là số nguyên với mọi số nguyên dương n và tìm số dư của s2018 khi chia cho 3.c) Chứng minh rằng [(2 + sqrt{3})^n] s_{n} - 1 với mọi số nguyên dương n, trong đó kí hiệu [x] là phần nguyên của số thực x.
Đọc tiếp
Với mỗi số nguyên dương \(n\), đặt \(s_{n} = (2 - \sqrt{3})^n + (2 + \sqrt{3})^n\)
a) Chứng minh rằng: \(s_{n+2} = 4s_{n+1} - s_{n}\)
b) Chứng minh rằng sn là số nguyên với mọi số nguyên dương n và tìm số dư của s2018 khi chia cho 3.
c) Chứng minh rằng \([(2 + \sqrt{3})^n] = s_{n} - 1\) với mọi số nguyên dương \(n\), trong đó kí hiệu [x] là phần nguyên của số thực \(x\).
Cho biểu thức
a) Tìm tập xác định của biểu thức A và rút gọn biểu thức A
b) Chứng minh A > 0 với mọi x khác 1
c) Tìm x để A đạt giá trị lớn nhất . Tìm GTLN đó
A = \(\left(\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}}{x+\sqrt{x}+1}+\frac{1}{1-\sqrt{x}}\right):\frac{\sqrt{x}-1}{2}\)
1.A=\(\dfrac{\sqrt{x}}{\sqrt{x}+3}\) và B=\(\dfrac{2\sqrt{x}}{\sqrt{x}-3}\) \(-\dfrac{3x+9}{x-9}\) với x ≥ 0,x ≠9
a) Tính giá trị biểu thức A khi x=16
b) Chứng minh A+3=\(\dfrac{3}{\sqrt{x}+3}\)
Mn giúp mk vs nhé ạ!!!