Ở lớp 8 ta đã làm quen với những hành động, thực nghiệm đơn giản, mà kết quả của chúng không thể biết được trước khi thực hiện. Trong bài học này, chúng ta sẽ gặp những hành động, thực nghiệm phức tạp hơn hoặc được tiến hành liên tiếp hay đồng thời.
Một cửa hàng muốn tặng hai phần quà cho hai trong bốn khách hàng có lượng mua nhiều nhất trong tháng bằng cách rút thăm ngẫu nhiên. Việc rút thăm được tiến hành như sau: Nhân viên viết tên 4 khách hàng đó vào 4 lá phiếu để vào một chiếc hộp. Nhân viên rút ngẫu nhiên một lá phiếu trong hộp. Lá phiếu rút ra không trả lại vào hộp. Sau đó, nhân viên tiếp tục rút ngẫu nhiên một lá phiếu từ ba lá phiếu còn lại. Hai khách hàng có tên trong hai lá phiếu được rút ra là hai khách hàng được tặng quà. Hỏi có bao nhiêu kết quả có thể xảy ra?
Phép thử là rút ngẫu nhiên lần lượt hai lá phiếu từ hộp, lá phiếu được rút ra lần đầu không trả lại vào hộp.
Kết quả của phép thử là một cặp tên (a, b), trong đó a và b tương ứng là tên khách hàng ghi trên lá phiếu được lấy ra ở lần thứ nhất và lần thứ hai. Vì lá phiếu được lấy ra lần đầu không trả lại vào hộp nên a ≠ b.
Kí hiệu bốn khách hàng có lượng mua nhiều nhất lần lượt là A, B, C và D.
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
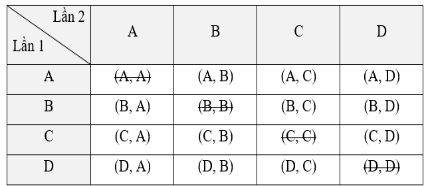
Vì a ≠ b nên cặp có hai phần tử trùng nhau không được tính, tức là trong bảng ta phải xóa 4 ô: (A, A); (B, B); (C, C); (D, D). Do đó không gian mẫu của phép thử là Ω = {(A, B); (A, C); (A, D); (B, A); (B, C); (B, D); (C, A); (C, B); (C, D); (D, A); (D, B); (D, C)}.
Vậy phép thử có 12 kết quả có thể xảy ra.


