Vận tốc tức thời của dao động: \(f'\left( x \right) = - \sin x\)
Vận tốc tức thời của vật tại thời điểm \({x_0} = 2\left( s \right)\):\(f'\left( 2 \right) = - \sin \left( 2 \right) = 0,91\left( {m/s} \right)\)
Vận tốc tức thời của dao động: \(f'\left( x \right) = - \sin x\)
Vận tốc tức thời của vật tại thời điểm \({x_0} = 2\left( s \right)\):\(f'\left( 2 \right) = - \sin \left( 2 \right) = 0,91\left( {m/s} \right)\)
Tính đạo hàm của hàm số \(f\left( x \right)= \log x\) tại điểm \({x_0} = \frac{1}{2}\)
Tính đạo hàm của hàm số \(f\left( x \right) = \sqrt x \) tại điểm \({x_0} = 9\)
Tính đạo hàm của hàm số \(f\left( x \right) = {10^x}\) tại điểm \({x_0} = - 1\)
Tính đạo hàm của hàm số \(f\left( x \right) = \tan x\) tại điểm \({x_0} = - \frac{\pi }{6}\)
Tính đạo hàm của hàm số \(f\left( x \right) = \cot x\) tại điểm \({x_0} = - \frac{\pi }{3}\)
Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu \({v_0} = 196m/s\) (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0. (lấy \(g = 9,8m/{s^2}\))
Viết phương trình tiếp tuyến của đồ thị hàm số sau:
a) \(y = {x^3} - 3{x^2} + 4\) tại điểm có hoành độ \({x_0} = 2\)
b) \(y = \ln x\) tại điểm có hoành độ \({x_0} = e\)
c) \(y = {e^x}\) tại điểm có hoành độ \({x_0} = 0\)
Tính đạo hàm của hàm số f(x) = sinx tại điểm \({x_0} = \frac{\pi }{2}\)
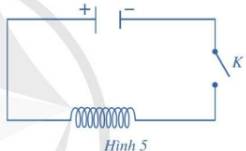
Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích \({Q_0}\). Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức \(q(t) = {Q_0}\sin \omega t\), trong đó \(\omega \) là tốc độ góc. Biết rằng cường độ I(t) của dòng diện tại thời điểm t được tính theo công thức \(I(t) = q'(t)\). Cho biết \({Q_0} = {10^{ - 8}}(C)\) và \(\omega = {10^6}\pi \,\,\,(rad/s)\). Tính cường độ của dòng điện tại thời điểm \(t = 6(s)\) (tính chính xác đến \({10^{ - 5}}(mA)\)