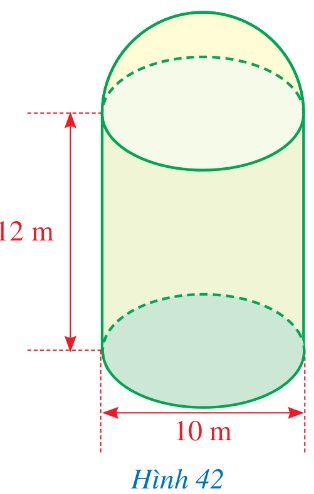
Một kho chứa ngũ cốc có dạng một hình trụ và một mái vòm có dạng nửa hình cầu. Phần hình trụ có đường kính đáy là 10 m và chiều cao là 12 m. Phần mái vòm là nửa hình cầu đường kính 10 m (Hình 42). Hỏi dung tích của kho đó là bao nhiêu mét khối (bỏ qua bề dày của tường nhà kho và làm tròn kết quả đến hàng phần trăm)?
Thể tích hình cầu có đường kính 10m là:
\(\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {\left( {\frac{{10}}{2}} \right)^3} = \frac{{1000\pi }}{3}\left( {{m^3}} \right).\)
Thể tích mái vòm có dạng nửa hình cầu là:
\(\frac{{1000\pi }}{3}:2 = \frac{{500\pi }}{3}\left( {{m^3}} \right).\)
Thể tích hình trụ là:
\(\pi {R^2}h = \pi {\left( {\frac{{10}}{2}} \right)^2}.12 = 300\pi \left( {{m^3}} \right).\)
Dung tích của kho là:
\(\frac{{500\pi }}{3} + 300\pi \approx 1465,33\left( {{m^3}} \right).\)


