Một kho chứa 60 tấn xi măng, mỗi ngày đều xuất đi m(tấn) với ) 0 < m < 60. Gọi y (tấn) là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.
a) Chứng tỏ rằng y là hàm số bậc nhất của biến x, tức là y = ax + b (a≠0).
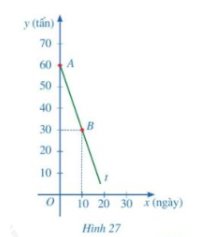
b) Trong hình 27, tia At là một phần đường thẳng y = ax + b. Tìm a,b. Từ đó hãy cho biết trong kho còn lại bao nhiêu tấn xi măng sau 15 ngày.
a) Theo đề bài, mỗi ngày xuất đi m (tấn) với 0 < m < 60.
=> x ngày xuất đi m.x (tấn).
Vậy khối lượng xi măng còn lại trong kho sau x ngày xuất hàng là:
60 - mx (tấn)
Mà y (tấn) là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.
=> y = 60 - mx hay y = -mx + 60 (m \( \ne \) 0)
Vậy y là hàm số bậc nhất của biến x (đpcm).
b) Từ hình 27, tia At đi qua hai điểm A(0; 60); B(10; 30)
Thay tọa độ điểm A(0; 60) vào hàm số bậc nhất y = ax + b \(\left( {a \ne 0} \right)\)ta được:
60 = a. 0 + b suy ra b = 60
Hàm số bậc nhất là y = ax + 60 (1)
Thay tọa độ B(10; 30) vào hàm số bậc nhất (1) ta có:
30 = a. 10 + 60 suy ra a = -3
Vậy y = -3x + 60
Với x = 15 ta có y = -3.15 + 60 = 15
Vậy trong kho còn lại 15 tấn xi măng sau 15 ngày.