SGK Cánh Diều - Tập 2 - Trang 97
26 tháng 7 lúc 12:22
Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét biết cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
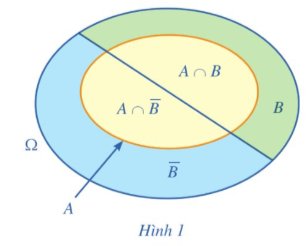
a) Viết các tập con của không gian mẫu tương ứng với các biến cố A, B, A ∩ B, A ∩ \(\overline{B}\) (Hình 1).
b) So sánh: n(A) và n(A ∩ B) + n(A ∩ \(\overline{B}\)).
Từ đó hãy chứng tỏ rằng: \(P\left(A\right)=P\left(A\cap B\right)+P\left(A\cap\overline{B}\right)\).
c) So sánh: P(A ∩ B) và P(B) . P(A | B); P(A ∩ \(\overline{B}\)) và P(\(\overline{B}\)) . P(A | \(\overline{B}\)).
