Các tứ giác trên là hình thoi vì có 4 cạnh bằng nhau
Chu vi của hoa văn là: \(2 \times 4 \times 3 = 24\) (cm)
Các tứ giác trên là hình thoi vì có 4 cạnh bằng nhau
Chu vi của hoa văn là: \(2 \times 4 \times 3 = 24\) (cm)
Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4cm và 5cm. Tìm độ dài hai cạnh còn lại.
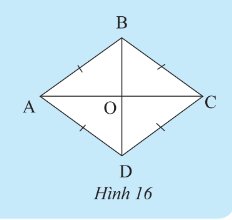
Một tứ giác có chu vi là \(52\) cm và một đường chéo là \(24\)cm. Tính độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
Một tứ giác có chu vi là \(52\) cm và một đường chéo là \(24\)cm. Tính độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
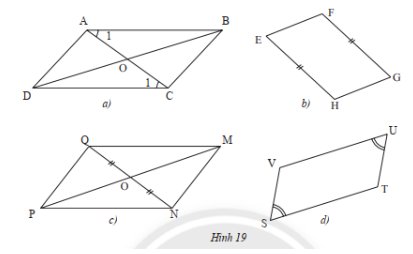
Hình 11a là hình chụp tấm lưới thép được đan thành nhiều mắt. Hình 11b là hình vẽ phóng to của một mắt lưới. Đo độ dài các cạnh của tứ giác \(ABCD\) và rút ra nhận xét.

Cho tứ giác \(ABCD\) có các cạnh đối song song. Gọi \(O\) là giao điểm của hai đường chéo. Hãy chứng tỏ:
- Tam giác \(ABC\) bằng tam giác \(CDA\)
- Tam giác \(OAB\) bằng tam giác \(OCD\)
Cho hình bình hành \(ABCD\). Gọi \(I\) và \(K\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD\); \(E\) và \(F\) lần lượt là giao điểm của \(AK\) và \(CI\) với \(BD\).
a) Chứng minh tứ giác \(AEFI\) là hình thang
b) Chứng minh \(DE = EF = FB\)
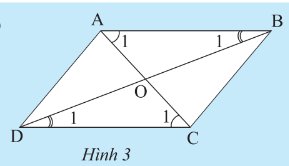
Cho \(ABCD\) là một hình bình hành. Giải thích tại sao tứ giác \(ABCD\) có bốn cạnh bằng nhau trong mỗi trường hợp sau:
Trường hợp 1: \(AB = AD\)
Trường hợp 2: \(AC\) vuông góc với \(BD\)
Trường hợp 3: \(AC\) là phân giác góc \(BAD\)
Trường hợp 4: \(BD\) là phân giác góc \(ABC\)
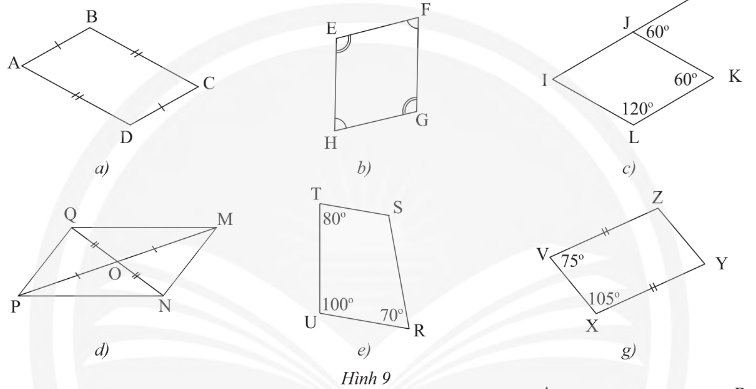
Trong các tứ giác ở Hình 9, tứ giác nào không là hình bình hành?
Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm của \(AD\), \(F\) là trung điểm của \(BC\)
a) Chứng minh rằng tứ giác \(EBFD\) là hình bình hành
b) Gọi \(O\) là giao điểm của hai đường chéo của hình bình hành \(ABCD\). Chứng minh rằng ba điểm \(E\), \(O\), \(F\) thẳng hàng.