Lời giải:
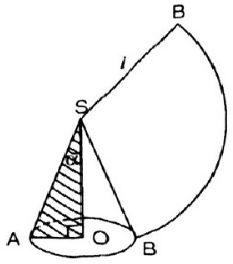
Gọi độ dài đường sinh hình nón là $l$
Diện tích xung quanh hình nón: $S_{xq}=\pi Rl$
Diện tích đáy: $S_{đáy}=\pi R^2$
Theo bài ra ta có: $\pi Rl=2\pi R^2$
$\Rightarrow l=2R$
Chiều cao của hình nón: $h=\sqrt{l^2-R^2}=\sqrt{(2R)^2-R^2}=\sqrt{3}R$
Thể tích hình nón là:
$V=\frac{1}{3}\pi R^2h=\frac{1}{3}.\pi. R^2.\sqrt{3}R=\frac{\sqrt{3}}{3}\pi R^3$