Từ câu a ta có AE=AF \(\Rightarrow\Delta AEF\) vuông cân tại A
\(\Rightarrow AI\) đồng thời là phân giác \(\widehat{FAE}\Rightarrow\widehat{KAF}=\dfrac{1}{2}\widehat{FAE}=\dfrac{1}{2}.90^0=45^0\)
Lại có ABCD là hình vuông \(\Rightarrow\widehat{ACF}=45^0\)
\(\Rightarrow\widehat{ACF}=\widehat{KAF}\)
Xét hai tam giác AKF và CAF có: \(\left\{{}\begin{matrix}\widehat{ACF}=\widehat{KAF}\\\widehat{AFC}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta AKF\sim\Delta CAF\left(g.g\right)\Rightarrow\dfrac{AF}{CF}=\dfrac{FK}{AF}\Rightarrow AF^2=KF.CF\)
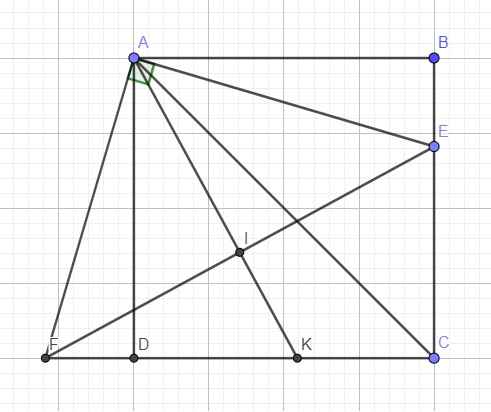
Cho h.vuông ABCD,điểm E tùy ý trên BC.Kẻ Ax vuông góc AE cắt CD kéo dài tại F.Kẻ trung tuyến AI của tam giác AEF và kéo dài cắt CD ở K
a) C/m AE =AF
b)C/m AF^2=KF.CF