Mô tả thuật toán tìm nghiệm của phương trình bậc hai tổng quát bằng cách liệt kê hoặc bằng sơ đồ khối.
Xác định bài toán:
•
– Input: Các số thực a, h, c (a≠0).
– Output: Các số thực X thoả mãn ax2 + bx + c = 0.
– Ý tưởng:
– Tính d = b2 – 4ac.
– Lần lượt xét ba trường hợp cho giá trị d:
nếu d
nếu d = 0 thì kết luận phương trình có một nghiệm x =-b/2a
nếu d > 0 thì kết luận phương trình có hai nghiệm phân biệt là:
x – (-b± √ d ) / 2a.
Thuật toán:
Mô tả thuật toán bằng cách liệt kê:
Bước I. Nhập ba số a, b, c;
Bước 2. d 4-(b*b – 4*a*c);
Bước 3.
nếu d < 0 thì đưa ra thông báo phương trình vô nghiệm rồi kết thúc;
nếu d = 0 thì đưa ra thông báo phương trình có một nghiệm và tính nghiệm
x = -b/(2*a), rồi kết thúc;
nếu (d> 0 thì đưa ra thông báo phương trình có hai nghiệm phân biệt, tính nghiệm X/= (-b + -√ d) / (2*a) và x2 = (-b – √ d ) / (2*a), rồi kết thúc;
Mô tả thuật toán theo sơ đồ khối:
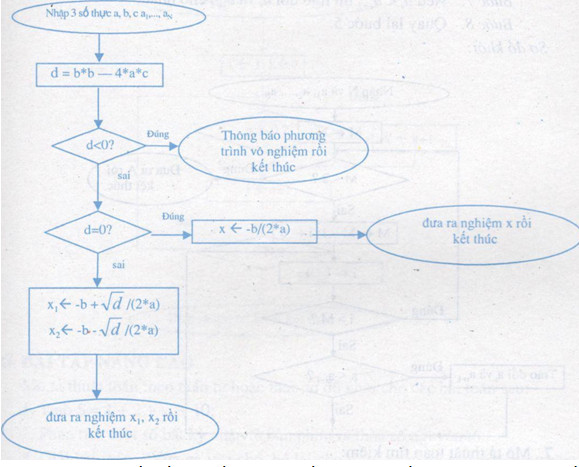
Xác định bài toán:
•
- Input: Các số thực a, h, c (a≠0).
- Output: Các số thực X thoả mãn ax2 + bx + c = 0.
- Ý tưởng:
- Tính d = b2 - 4ac.
- Lần lượt xét ba trường hợp cho giá trị d:
nếu d
nếu d = 0 thì kết luận phương trình có một nghiệm x =-b/2a
nếu d > 0 thì kết luận phương trình có hai nghiệm phân biệt là:
x - (-b± √ d ) / 2a.
Thuật toán:
Mô tả thuật toán bằng cách liệt kê:
Bước I. Nhập ba số a, b, c;
Bước 2. d 4-(b*b - 4*a*c);
Bước 3.
nếu d < 0 thì đưa ra thông báo phương trình vô nghiệm rồi kết thúc;
nếu d = 0 thì đưa ra thông báo phương trình có một nghiệm và tính nghiệm
x = -b/(2*a), rồi kết thúc;
nếu (d> 0 thì đưa ra thông báo phương trình có hai nghiệm phân biệt, tính nghiệm X/= (-b + -√ d) / (2*a) và x2 = (-b - √ d ) / (2*a), rồi kết thúc;
Mô tả thuật toán theo sơ đồ khối:
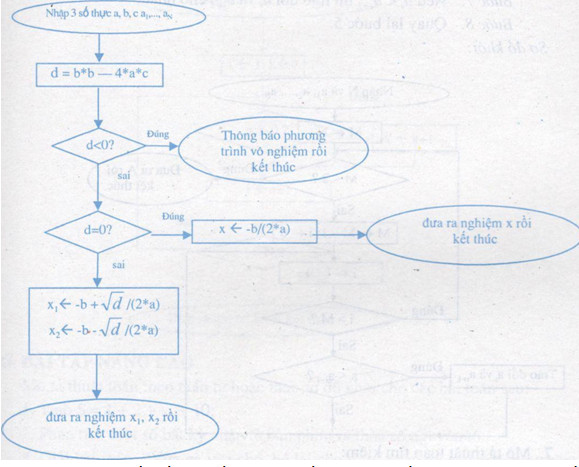
Mô tả thuật toán tìm nghiệm của phương trình bậc hai tổng quát bằng cách liệt kê hoặc bằng sơ đồ khối.
Xác định bài toán:
•
– Input: Các số thực a, h, c (a≠0).
– Output: Các số thực X thoả mãn ax2 + bx + c = 0.
– Ý tưởng:
– Tính d = b2 – 4ac.
– Lần lượt xét ba trường hợp cho giá trị d:
nếu d
nếu d = 0 thì kết luận phương trình có một nghiệm x =-b/2a
nếu d > 0 thì kết luận phương trình có hai nghiệm phân biệt là:
x – (-b± √ d ) / 2a.
Thuật toán:
Mô tả thuật toán bằng cách liệt kê:
Bước I. Nhập ba số a, b, c;
Bước 2. d 4-(b*b – 4*a*c);
Bước 3.
nếu d < 0 thì đưa ra thông báo phương trình vô nghiệm rồi kết thúc;
nếu d = 0 thì đưa ra thông báo phương trình có một nghiệm và tính nghiệm
x = -b/(2*a), rồi kết thúc;
nếu (d> 0 thì đưa ra thông báo phương trình có hai nghiệm phân biệt, tính nghiệm X/= (-b + -√ d) / (2*a) và x2 = (-b – √ d ) / (2*a), rồi kết thúc;
Mô tả thuật toán theo sơ đồ khối:


















