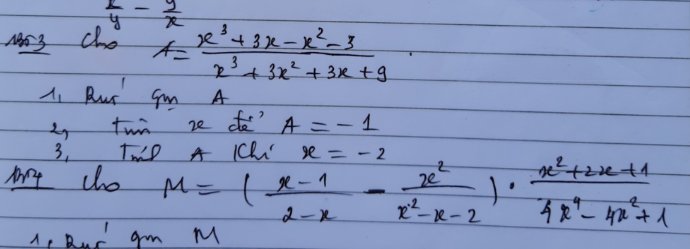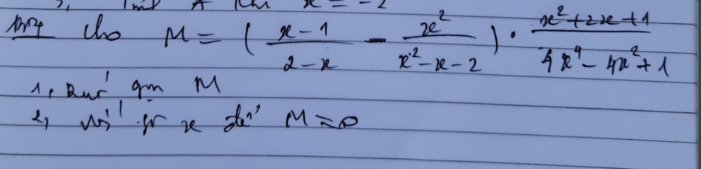Bài 1. (a) Điều kiện: \(x\ne\pm1\).
Ta có: \(A=\left(\dfrac{x-2}{x-1}-\dfrac{x+3}{x+1}+\dfrac{3}{x-1}\right):\left(1-\dfrac{x+3}{x+1}\right)\)
\(=\left(\dfrac{x-2+3}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-\left(x+3\right)}{x+1}\)
\(=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-x-3}{x+1}\)
\(=\dfrac{\left(x+1\right)^2-\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{-2}{x+1}\)
\(=\dfrac{x^2+2x+1-x^2-2x+3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}\)
\(=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}=\dfrac{2}{1-x}\)
Vậy: \(A=\dfrac{2}{1-x}\)
(b) \(A=3\Leftrightarrow\dfrac{2}{1-x}=3\)
\(\Rightarrow1-x=\dfrac{2}{3}\Leftrightarrow x=\dfrac{1}{3}\left(TM\right)\)
Vậy: \(x=\dfrac{1}{3}\)
Bài 2. (a) Phương trình tương đương với:
\(\dfrac{3\left(3x-2\right)}{12}+\dfrac{6\left(x+3\right)}{12}=\dfrac{4\left(x-1\right)}{12}+\dfrac{x+1}{12}\)
\(\Rightarrow3\left(3x-2\right)+6\left(x+3\right)=4\left(x-1\right)+x+1\)
\(\Leftrightarrow9x-6+6x+18=4x-4+x+1\)
\(\Leftrightarrow10x=-15\Leftrightarrow x=-\dfrac{3}{2}\)
Vậy: Phương trình có tập nghiệm \(S=\left\{-\dfrac{3}{2}\right\}\).
(b) Điều kiện: \(x\ne\pm1\). Phương trình tương đương với:
\(\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2x^2+2}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow2\left(x+1\right)+2\left(x-1\right)=2x^2+2\)
\(\Leftrightarrow2x+2+2x-2=2x^2+2\)
\(\Leftrightarrow2x^2-4x+2=0\Leftrightarrow2\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow2\left(x-1\right)^2=0\Rightarrow x-1=0\Leftrightarrow x=1\left(KTM\right)\)
Vậy: Phương trình có tập nghiệm \(S=\varnothing\)
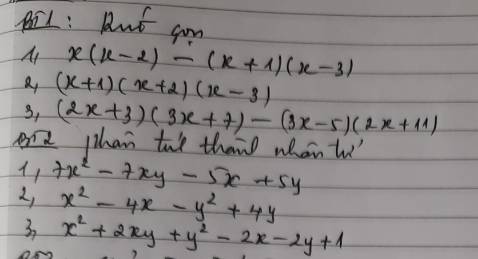
mn giup mik bai 3 nay dc ko aj
