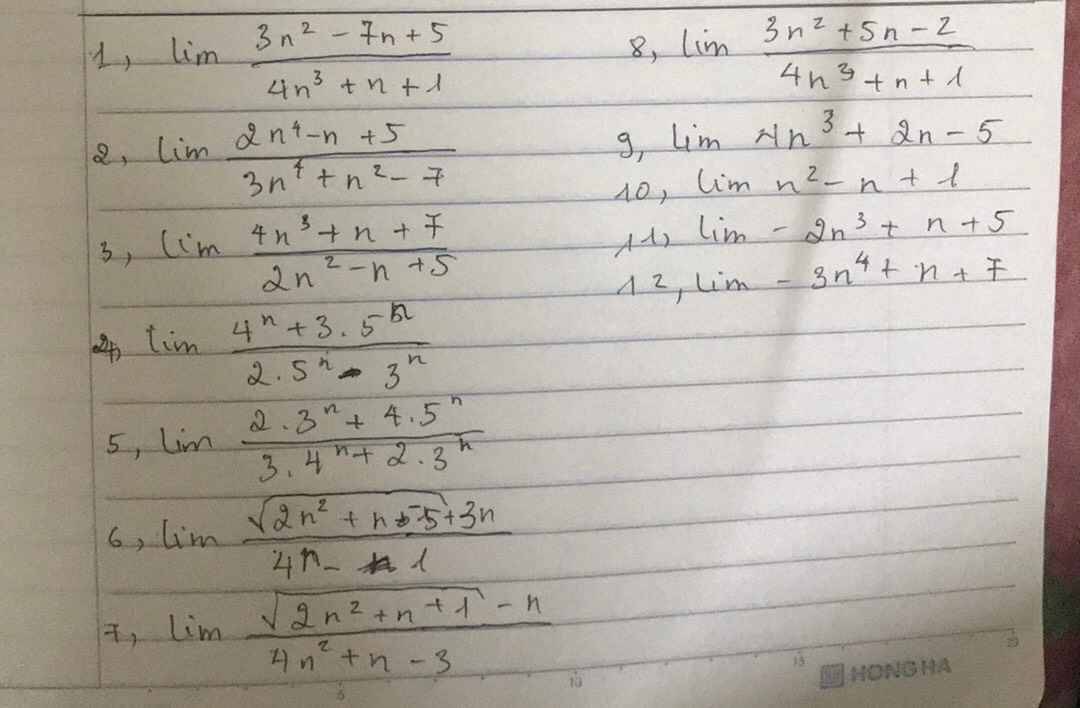1: \(=lim\left(\dfrac{\dfrac{3}{n}-\dfrac{7}{n^2}+\dfrac{5}{n^3}}{4+\dfrac{1}{n^2}+\dfrac{1}{n^3}}\right)=0\)
2: \(=lim\left(\dfrac{2-\dfrac{1}{n^3}+\dfrac{5}{n^4}}{3+\dfrac{1}{n^2}-\dfrac{7}{n^4}}\right)=\dfrac{2}{3}\)
3: \(=lim\left(\dfrac{4+\dfrac{1}{n^2}+\dfrac{7}{n^3}}{\dfrac{2}{n}-\dfrac{1}{n^2}+\dfrac{5}{n^3}}\right)=+\infty\)
4: \(=lim\left(\dfrac{\left(\dfrac{4}{5}\right)^n+3}{2-\left(\dfrac{3}{5}\right)^n}\right)=\dfrac{3}{2}\)
5: \(=lim\left(\dfrac{2\cdot\left(\dfrac{3}{5}\right)^n+4}{3\cdot\left(\dfrac{4}{5}\right)^n+2\cdot\left(\dfrac{3}{5}\right)^n}\right)=+\infty\)
6: \(=lim\left(\dfrac{\sqrt{2+\dfrac{1}{n}-\dfrac{5}{n^2}}+3}{4-\dfrac{1}{n}}\right)=\dfrac{3}{4}\)
7: \(=lim\left(\dfrac{\sqrt{\dfrac{2}{n^2}+\dfrac{1}{n^3}+\dfrac{1}{n^4}}-\dfrac{1}{n}}{4+\dfrac{1}{n}-\dfrac{3}{n^2}}\right)=+\infty\)
\(8,lim\dfrac{3n^2+n-2}{4n^3+n+1}\)
\(=lim\dfrac{\dfrac{3n^2}{n^3}+\dfrac{n}{n^3}-\dfrac{2}{n^3}}{\dfrac{4n^3}{n^3}+\dfrac{n}{n^3}+\dfrac{1}{n^3}}\)
\(=lim\dfrac{\dfrac{3}{n}+\dfrac{1}{n^2}-\dfrac{2}{n^3}}{4+\dfrac{1}{n^2}+\dfrac{1}{n^3}}\)
\(=\dfrac{0}{4}\)
\(=0\)
\(9,lim4n^3+2n-5\)
\(=lim\left(\dfrac{4n^3}{n^3}+\dfrac{2n}{n^3}-\dfrac{5}{n^3}\right)\)
\(=lim\left(4+\dfrac{2}{n^2}-\dfrac{5}{n^3}\right)\)
\(=4\)
\(10,lim\left(n^2-n+1\right)\)
\(=lim\left(\dfrac{n^2}{n^2}-\dfrac{n}{n^2}+\dfrac{1}{n^2}\right)\)
\(=lim\left(1-\dfrac{1}{n}+\dfrac{1}{n^2}\right)\)
\(=1\)
\(11,lim\left(-2n^3+n+5\right)\)
\(=lim\left(-\dfrac{2n^3}{n^3}+\dfrac{n}{n^3}+\dfrac{5}{n^3}\right)\)
\(=lim\left(-2+\dfrac{1}{n^2}+\dfrac{5}{n^3}\right)\)
\(=-2\)
\(12,lim\left(-3n^4+n+7\right)\)
\(=lim\left(-\dfrac{3n^4}{n^4}+\dfrac{n}{n^4}+\dfrac{7}{n^4}\right)\)
\(=lim\left(-3+\dfrac{1}{n^3}+\dfrac{7}{n^4}\right)\)
\(=-3\)