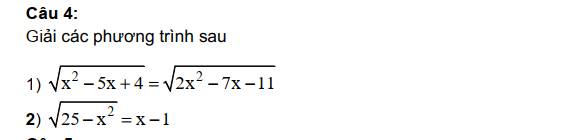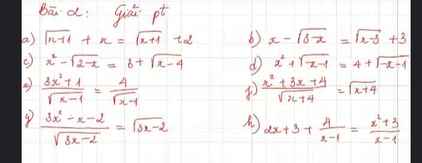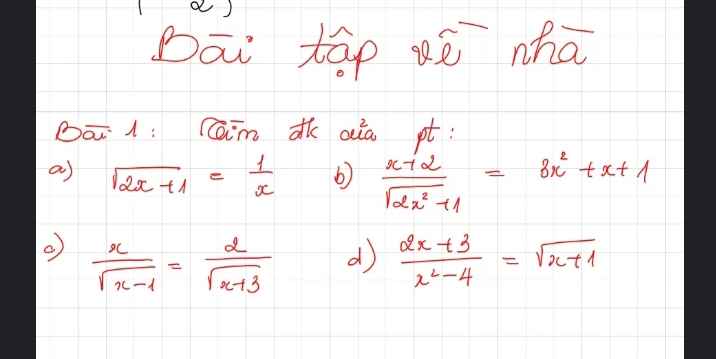ĐKXĐ: ...
\(\Leftrightarrow\sqrt{x-1}+\sqrt{x+3}+2x+2+2\sqrt{\left(x-1\right)\left(x+3\right)}-6=0\)
Đặt \(\sqrt{x-1}+\sqrt{x+3}=t>0\)
\(\Rightarrow t^2=2x+2+2\sqrt{\left(x-1\right)\left(x+3\right)}\)
Phương trình trở thành:
\(t+t^2-6=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-3\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-1}+\sqrt{x+3}=2\)
\(\Leftrightarrow\sqrt{x-1}+\sqrt{x+3}-2=0\)
\(\Leftrightarrow\sqrt{x-1}+\dfrac{x-1}{\sqrt{x+3}+2}=0\)
\(\Leftrightarrow\sqrt{x-1}\left(1+\dfrac{\sqrt{x-1}}{\sqrt{x+3}+2}\right)=0\)
\(\Leftrightarrow\sqrt{x-1}=0\)
\(\Leftrightarrow x=1\)
Đúng 1
Bình luận (1)
giúp mình câu này với ạ