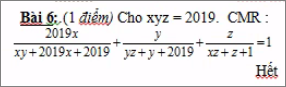\(\dfrac{2019x}{xy+2019x+2019}+\dfrac{y}{yz+y+2019}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{2019xz}{xyz+2019xz+2019z}+\dfrac{xz.y}{xz.yz+xz.y+2019xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{2019xz}{2019+2019xz+2019z}+\dfrac{2019}{2019z+2019+2019xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}\)
\(=\dfrac{xz+z+1}{xz+z+1}=1\)