Khối lượng q (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán p (nghìn đồng/kg) theo công thức \(p=15-\dfrac{1}{2}q\). Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức R = pq.
a) Viết công thức biểu diễn R theo p.
b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.
a) Ta có: \(p = 15 - \frac{1}{2}q \Leftrightarrow q = 2(15 - p)\)
Thay vào \(R = pq\) ta được: \(R = p.2(15 - p) = - 2{p^2} + 30p\)
b) Đặt \(y = - 2{p^2} + 30p\)
Tập xác định: \(D = (0; + \infty )\)
\(y' = - 4p + 30 = 0 \Leftrightarrow p = 7,5\)
Bảng biến thiên:
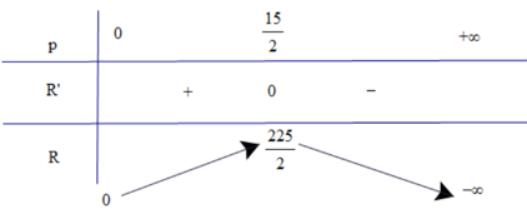
Từ bảng biến thiên, ta thấy \(\mathop {\max }\limits_D y = y(7,5) = 112,5\)
Vậy nếu giá bán mỗi kilôgam sản phẩm là 7,5 nghìn đồng/kg thì sẽ đạt được doanh thu cao nhất là 112,5 nghìn đồng


