Lời giải:
Ta thấy
$\Delta'=(m+1)^2-(2m+1)=m^2\geq 0$ với mọi $m\in\mathbb{R}$ nên pt luôn có 2 nghiệm $x_1,x_2$
Áp dụng định lý Viet:
$x_1+x_2=2(m+1)$
$x_1x_2=2m+1$
$x_1,x_2\neq 0\Leftrightarrow x_1x_2=2m+1\neq 0$
$\Leftrightarrow m\neq \frac{-1}{2}$
Từ hệ thức Viet ta có:
$\frac{1}{x_1^2}+\frac{1}{x_2^2}=\frac{10}{9}$
$\Leftrightarrow (\frac{1}{x_1}+\frac{1}{x_2})^2-\frac{2}{x_1x_2}=\frac{10}{9}$
$\Leftrightarrow \frac{(x_1+x_2)^2}{(x_1x_2)^2}-\frac{2}{x_1x_2}=\frac{10}{9}$
$\Leftrightarrow \frac{4(m+1)^2}{(2m+1)^2}-\frac{2}{2m+1}=\frac{10}{9}$
$\Leftrightarrow 9(4m^2+4m+2)=10(4m^2+4m+1)$
$\Leftrightarrow m^2+m-2=0$
$\Leftrightarrow (m-1)(m+2)=0$
$\Leftrightarrow m=1$ hoặc $m=-2$ (tm)

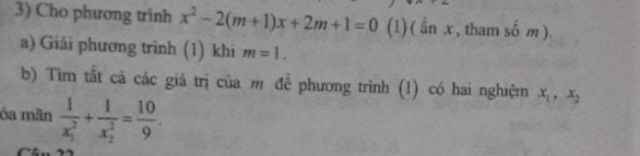 Hướng dẫn em cách làm phần b với ạ :
Hướng dẫn em cách làm phần b với ạ :


















