Hướng dẫn giải:
a) Diện tích hình tròn (O;R1) là S1 = πR12.
Diện tích hình tròn (O;R2) là S2 = πR22.
Diện tích hình vành khăn là:
S = S1 – S2 = πR12- πR22 = π( R12 – R22)
b) Thay số: S = 3,14. (10,52 – 7,82) = 155,1(cm2)
Hướng dẫn giải:
a) Diện tích hình tròn (O;R1) là S1 = πR12.
Diện tích hình tròn (O;R2) là S2 = πR22.
Diện tích hình vành khăn là:
S = S1 – S2 = πR12- πR22 = π( R12 – R22)
b) Thay số: S = 3,14. (10,52 – 7,82) = 155,1(cm2)
Cho tam giác ABC vuông ở A và đường cao AH. Vẽ đường tròn tâm O đường kính AB. Biết BH = 2cm, HC = 6cm. Tính :
a) Diện tích hình tròn (O)
b) Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ)
c) Diện tích hình quạt tròn AOH (ứng với cung nhỏ AH)
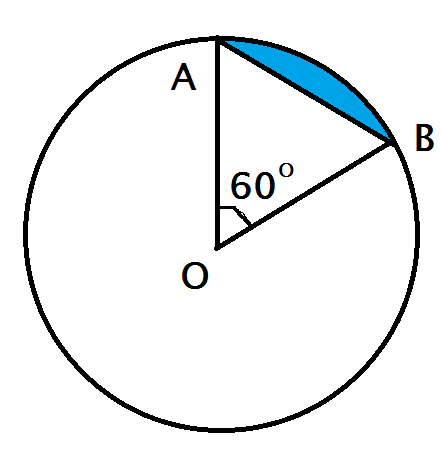
Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm \(\widehat{AOB}=60^o\) và bán kính đường tròn là 5,1 cm.
1. Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình quạt tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^o\)
2. Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm nội tiếp đường tròn (O). Tính diện tích hình tròn (O)
Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình tròn giới hạn tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^0\)
Tính diện tích hình tròn nội tiếp một hình vuông có cạnh là 4 cm.
Tính diện tích một hình quạt tròn có bán kính 6 cm, số đo cung là 36o.
Cho tam giác ABC nội tiếp đường tròn (O; R) có \(\widehat{C}=45^0\) :
a) Tính diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
b) Tính diện tích hình viên phân AmB (ứng với cung nhỏ AB)
Cho đường tròn (O; R). Chia đường tròn này thành ba cung có số đo tỉ lệ với 3, 4 và 5 rồi tính diện tích các hình quạt tròn được tạo thành ?
a) Tính diện tích hình tròn nội tiếp tam giác đều có độ dài mỗi cạnh 3cm b) Tính diệntích hình tròn ngoại tiếp ngũ giác đều có độ dài mỗi cạnh 4dm