Bài 10: Diện tích hình tròn
Nội dung lý thuyết
Các phiên bản khác1. Công thức tính diện tích hình tròn
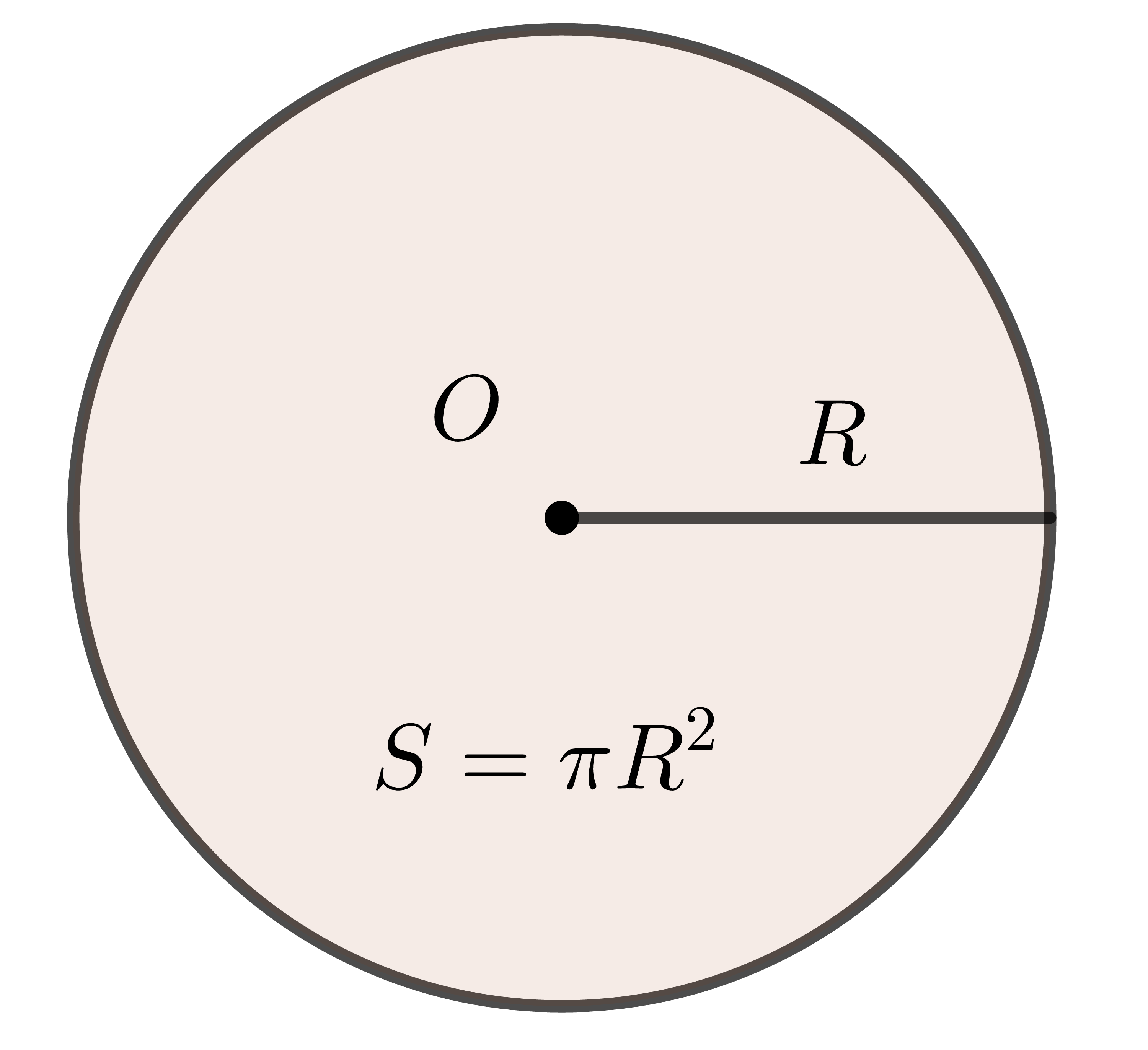
Kí hiệu diện tích hình tròn bán kính \(R\) là \(S\). Khi đó, diện tích hình tròn được tính bởi công thức:
\(S=\pi R^2\)
Ví dụ 1: Diện tích hình tròn bán kính \(5cm\) là: \(S=\pi5^2=25\pi\left(cm^2\right)\).
Ví dụ 2: Một hình tròn có diện tích là \(10\pi\left(m^2\right)\) thì có bán kính thỏa mãn \(\pi R^2=10\pi\Rightarrow R=\sqrt{10}\left(m\right)\).
@59909@
2. Cách tính diện tích hình quạt tròn
+) Hình quạt tròn là một phần hình tròn, giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó.
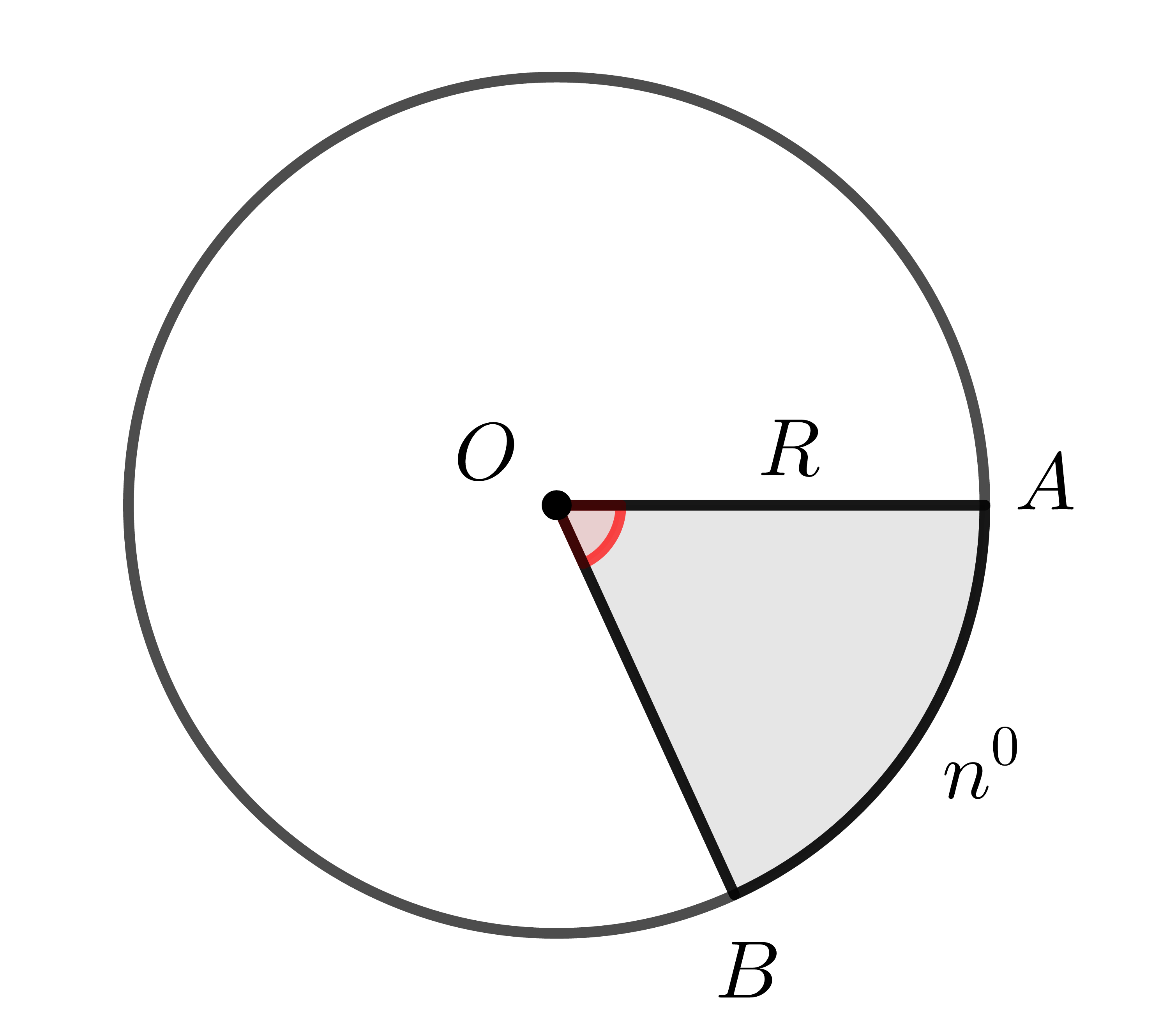
Trong hình trên, ta có hình quạt tròn \(OAB\), tâm \(O\), bán kính \(R\), cung \(n^0\).
+) Ta đã biết: Hình tròn bán kính \(R\) (ứng với \(360^0\)) có diện tích là \(\pi R^2\)
\(\Rightarrow\) Hình quạt tròn bán kính \(R\), cung \(1^0\) có diện tích là: \(\dfrac{\pi R^2}{360}\).
\(\Rightarrow\) Hình quạt tròn bán kính \(R\), cung \(n^0\) có diện tích là: \(S=\dfrac{\pi R^2n}{360}\).
Mặt khác, độ dài \(l\) của cung tròn \(n^0\) là \(l=\dfrac{\pi Rn}{180}\)
\(\Rightarrow S=\dfrac{\dfrac{\pi Rn}{180}.R}{2}=\dfrac{lR}{2}\).
Kết luận:
Diện tích hình quạt tròn bán kính \(R\), cung \(n^0\) được tính theo công thức:
\(S=\dfrac{\pi R^2n}{360}\) hay \(S=\dfrac{lR}{2}\)
(\(l\) là độ dài cung \(n^0\) của hình quạt tròn).
Ví dụ: Cho đường tròn \(\left(O;3cm\right)\). Hai điểm \(A,B\) thuộc đường tròn sao cho \(\widehat{AOB}=60^0\). Khi đó, số đo cung nhỏ \(AB\) là \(60^0\). Diện tích hình quạt tròn \(OAB\) là: \(S=\dfrac{\pi.3^2.60}{360}=\dfrac{3\pi}{2}\left(cm^2\right)\).
@59919@@59920@@59910@