Giải:
Theo bài 16 thì bán kính đường tròn chứa hình quạt độ dài bằng đường sinh của hình nón.
Đầu bài cho bán kính hình tròn chưa hình quạt là 16 cm nên độ dài đường sinh là 16 cm.
Vậy chọn A
Giải:
Theo bài 16 thì bán kính đường tròn chứa hình quạt độ dài bằng đường sinh của hình nón.
Đầu bài cho bán kính hình tròn chưa hình quạt là 16 cm nên độ dài đường sinh là 16 cm.
Vậy chọn A
Hình khai triển của mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là 16 cm, số đo cung là 120o. Tan của nửa góc ở đỉnh của hình nón là:
(A) \(\dfrac{\sqrt{2}}{4};\) (B) \(\dfrac{\sqrt{2}}{2};\) (C) \(\sqrt{2};\) (D) \(2\sqrt{2};\)
Hãy chọn kết quả đúng.
Cắt mặt xung quanh của hình nón trụ dọc theo một đường sinh của nó rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình nón trụ là một hình quạt tròn. Hình này bán kính r1 =25 r2 =35 độ dài đường sinh=36 hỏi độ dài cung tròn r1 và r2 là bao nhiêu, tính bán kidnh 2 cung tròn
Khi quay tam giác vuông để tạo ra một hình nón như ở hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là 30o, độ dài đường kính là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
Hình 101 :
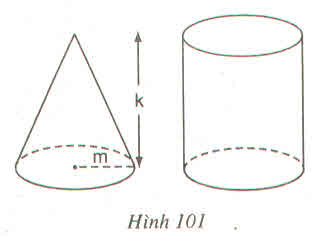
Có một hình nón, chiều cao k (cm), bán kính đường tròn đáy m(cm) và một hình trụ có cùng chiều cao và bán kính đường tròn đáy với hình nón. Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là :
(A) \(\dfrac{k}{4}cm\) (B) \(\dfrac{k}{3}cm\)
(C) \(\dfrac{2k}{3}cm\) (D) \(\dfrac{3k}{4}cm\)
Hãy chọn kết quả đúng ?
Hình 98:
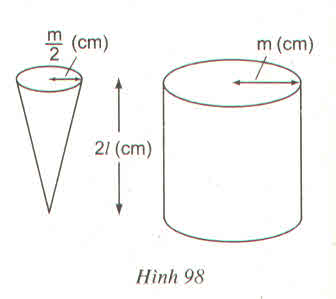
Có một hình nón, bán kính đường tròn đáy là \(\dfrac{m}{2}\left(cm\right)\), chiều cao là 2l (cm) và một hình trụ, bán kính đường tròn đáy m(cm), chiều cao 2l (cm). Người ta mức đầy nước vào hình nón và đổ vào hình trụ (không chứa gì cả) thì độ cao của nước trong hình trụ là :
(A) \(\dfrac{l}{6}\left(cm\right)\)
(B) \(l\left(cm\right)\)
(C) \(\dfrac{5}{6}l\left(cm\right)\)
(D) \(\dfrac{11}{6}l\left(cm\right)\)
Hãy chọn kết quả đúng ?
Hình 99 là một hình nón :
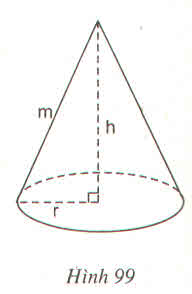
Chiều cao h (cm), bán kính đường tròn đáy là r (cm) và độ dài đường sinh m(cm) thì thể tích hình nón này là :
(A) \(\pi r^2h\left(cm^3\right)\) (B) \(\dfrac{1}{3}\pi r^2h\left(cm^3\right)\)
(C) \(\pi rm\left(cm^3\right)\) (D) \(\pi r\left(r+m\right)\left(cm^3\right)\)
Hãy chọn kết quả đúng ?
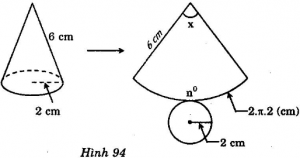
Cắt mặt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết basnk ính hình quạt tròn bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.
Quan sát hình 94 và tính số đo cung của hình quạt tròn.
Một hình trụ có bán kính đáy 1cm và chiều cao 2cm, người ta khoan đi một phần có dạng hình nón như hình vẽ (h.100) thì phần thể tích còn lại của nó sẽ là :
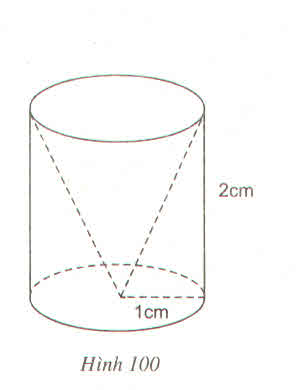
(A) \(\dfrac{2\pi}{3}\left(cm^3\right)\) (B) \(\dfrac{4\pi}{3}\left(cm^3\right)\)
(C) \(2\pi\left(cm^3\right)\) (D) \(\dfrac{8\pi}{3}\left(cm^3\right)\)
Hãy chọn kết quả đúng ?
Cối xay gió của Đôn-ki-hô-tê (từ tác phẩm của Xec-van-tec).
Phần trên của cối xay gió có dạng một hình nón. Chiều cao của hình nón là 42 cm và thể tích của nó là 17 600 cm3.
Em hãy tính giúp chàng Đôn-ki-hô-tê tính bán kính đáy của hình tròn (làm tròn kết quả đến chữ số thập phân thứ hai).
