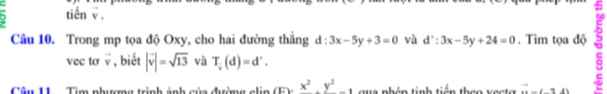Question

Helppppppp pleaseeeee

Answer 1

3:

Goi điểm B(x;y) thuộc d

Phép tịnh tiến biến B thành B'(x'y') thuộc d'

\(\left\{{}\begin{matrix}x'=x-1\\y'=y-2\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=x'+1\\y=y'+2\end{matrix}\right.\) <=>B(x'+1;y'+2)

Thay B vào d:

x'+1-(y'+2)+1=0<=> x'-y'=0

Vậy ảnh của d là d':y'=x'

4.

Cho điểm A(x'y') thuộc d

Phép quay tâm O góc -90^o biến A thành A'(x;y) thuộc d'

<=>\(\left\{{}\begin{matrix}x'=-y\\y'=x\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}y=-x'\\x=y'\end{matrix}\right.\)<=> A'(y'-x')

Thay A' vào d':

3y'+x'+4=0

Thay A và

Vậy phương trình đường thẳng d:x'+3y'+4=0 qua phép quay thành d'

5.

Gọi M(x;y) thuộc d

phép vị tự tâm I(2;3) tỉ số -1/3 biến M thành M'(x'y')

<=>\(\left\{{}\begin{matrix}x'=2+\dfrac{-1}{3}\left(x-2\right)\\y'=3+\dfrac{-1}{3}\left(y-3\right)\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=8-3x'\\y=12-3y'\end{matrix}\right.\)<=> M(8-3x'12-3y')

Thay M vào d

12-3y'=24-9x'-1<=>3y'=9x'-11

Vậy d' là 3y'=9x'-11

6) I(-3;4) là tâm đường tròn C

Phép quay biến (C) thành (C') và I'(x'y')

<=>\(\left\{{}\begin{matrix}x'=-3.cos\left(270\right)-4.sin\left(270\right)\\y'=-3.sin\left(270\right)+4.cos\left(270\right)\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x'=4\\y'=3\end{matrix}\right.\)

<=>I'(4;3)<=>(C'): (x-4)²+(y-3)²=3

7) E(0;-2) là tâm (C)

Phép vị tự tâm \(\overrightarrow{v}=\left(-4;-3\right)\) Biến E thành E'(x'y')

\(\left\{{}\begin{matrix}x'=0-4=-4\\y'=2-3=-1\end{matrix}\right.\)

Từ đó (C'): (x+4)²+(y+1)²=4

8) (C) \(\left(x-\dfrac{5}{2}\right)^2+\left(y-3\right)^2=\dfrac{69}{4}\)

<=>R=\(\dfrac{\sqrt{69}}{2}\) và I(5/2;3)

Phép vị tự tâm A tỉ số -2 biến I thành I'(x'y')

\(\left\{{}\begin{matrix}x'=1-2.\left(\dfrac{5}{2}-1\right)\\y'=5-2.\left(3-5\right)\end{matrix}\right.< =>\left\{{}\begin{matrix}x'=-2\\y'=9\end{matrix}\right.\)

<=>I'(-2;9) và R'=|-2|.2=4

(C') (x+2)²+(y-9)²=16