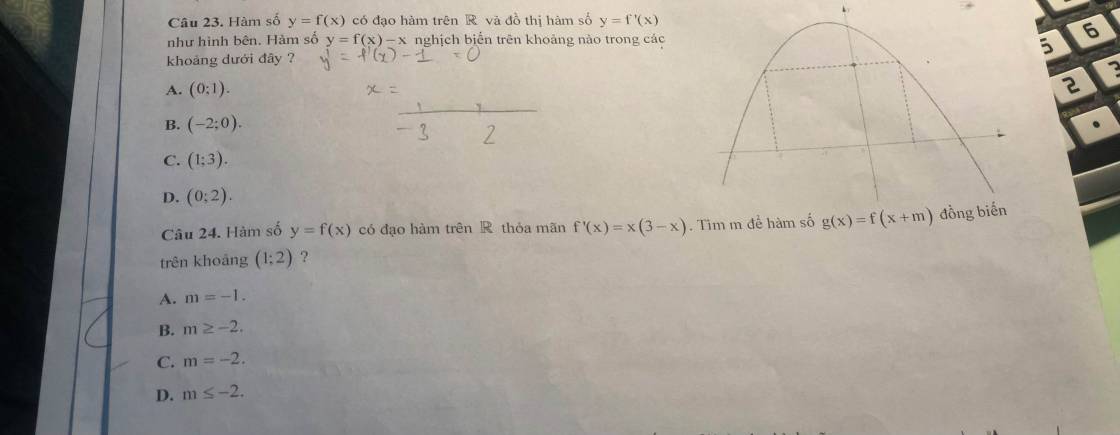\(g'\left(x\right)=3f'\left(3x+1\right)-6x+1\ge0\)
\(\Rightarrow f'\left(3x+1\right)\ge\dfrac{6x-1}{3}\)
Đặt \(3x+1=t\Rightarrow f'\left(t\right)\ge\dfrac{2t-3}{3}\)
Vẽ đường thẳng \(y=\dfrac{2t-3}{3}\) (đi qua 2 điểm (1;3), (0,-1) và (-3;-3)) lên cùng hệ trục với đồ thị \(f'\left(t\right)\)
Ta thấy \(f'\left(t\right)\ge\dfrac{2t-3}{3}\) khi \(\left[{}\begin{matrix}t\le-3\\0\le t\le3\end{matrix}\right.\)
\(\Rightarrow g\left(x\right)\) đồng biến khi: \(\left[{}\begin{matrix}3x+1\le-3\\0\le3x+1\le3\\\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\le-\dfrac{4}{3}\\-\dfrac{1}{3}\le x\le\dfrac{2}{3}\end{matrix}\right.\)
Do \(\left(0;\dfrac{2}{3}\right)\in\left[-\dfrac{1}{3};\dfrac{2}{3}\right]\) nên B đúng