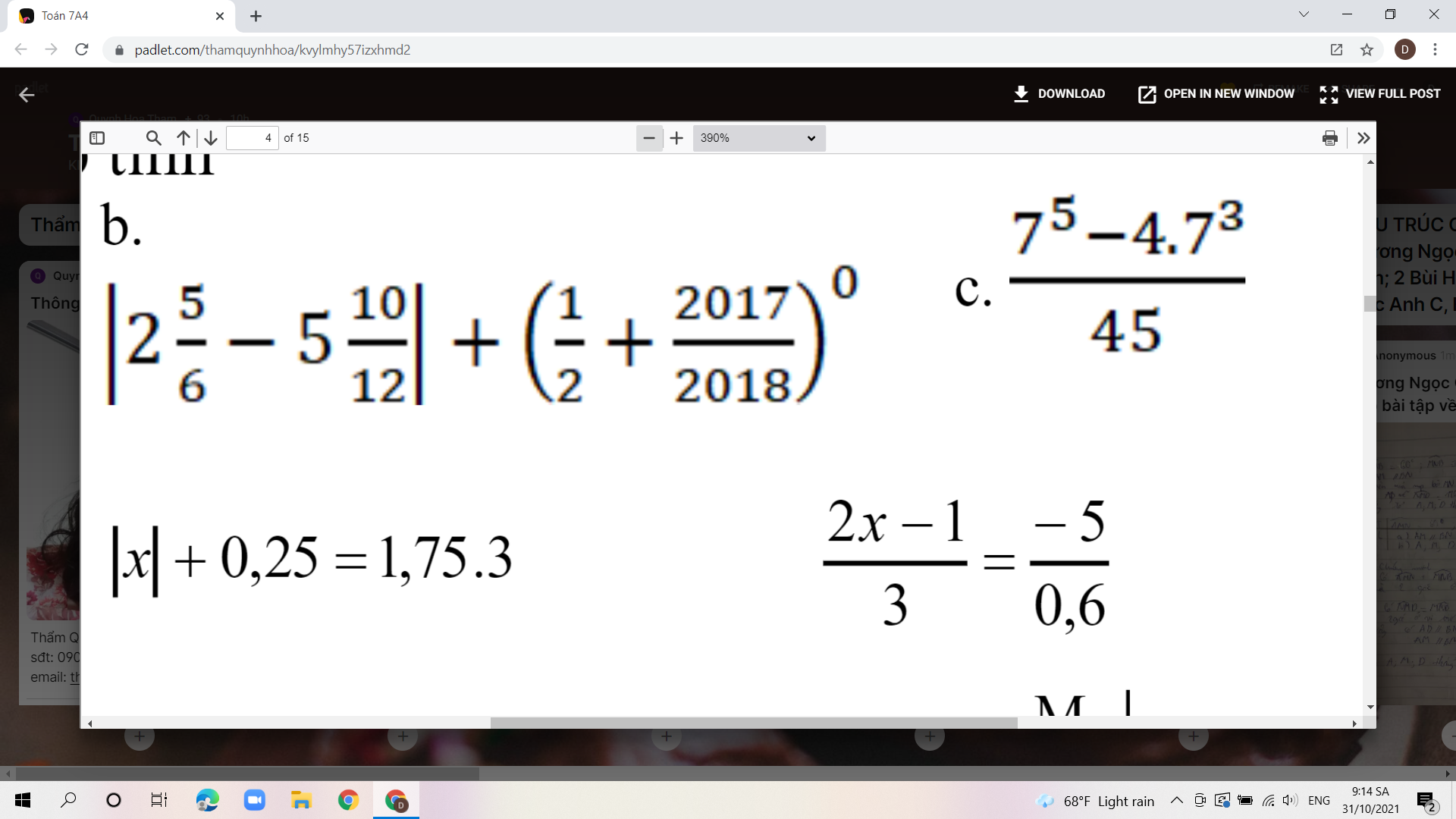
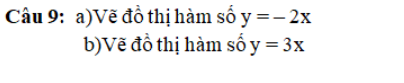Bài 2:i 2:
a/Xét t/g AMB và t/g AMC có:
AM : cạnh chung
MB = MC (gt)
AB = AC (gt)
=> t/g AMB = t/g AMC (c.c.c)
b/ Vì t/g AMB = t/g AMC (ý a)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^o\) (kề bù)
=> \(\widehat{AMB}=\widehat{AMC}=90^o\)
=> AM \(\perp\) BC
Có: \(\widehat{AMB}=\widehat{MAN}=90^o\)
mà 2 góc này ở vị trí so le trong nên:
=> a // BC
c/ Xét t/g AMC và t/g CNA có:
\(\widehat{MAC}=\widehat{NCA}\) (so le trong do b // AM)
AC: Cạnh chung
\(\widehat{MCA}=\widehat{NAC}\) (so le trong do b // AM)
=> t/g AMC = t/g CNA (g.c.g)
d/ Xét t/g AIN và t/g CIM có:
\(\widehat{IAN}=\widehat{ICM}\) (so le trong do b // AM)
AI = CI (gt)
\(\widehat{INA}=\widehat{IMC}\) (so le trong do b // AM)
=> t/g AIN = t/g CIM (g.c.g)
=> IN = IM (2 cạnh tương ứng)
=> I là trung điểm của đoạn thẳng MN
Bài 3:
a/ Xét t/g MAB và t/g MDC có:
MA = MD (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
MB = MC (gt)
=> t/g MAB = t/g MDC (c.g.c)
b/ Vì t/g MAB = t/g MDC (ý a)
=> AB = CD (2 cạnh tương ứng)
và \(\widehat{ABM}=\widehat{DCM}\) (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong nên:
=> AB // CD
c/ Vì AB // CD
=> \(\widehat{BAM}=\widehat{CDM}\) (so le trong)
\(\widehat{CAM}=\widehat{BDM}\) (so le trong)
=> \(\widehat{BAM}+\widehat{CAM}=\widehat{CDM}+\widehat{BDM}\)
hay \(\widehat{BAC}=\widehat{CDB}\)
d/ Xét t/g AME và t/g DMF có:
MA = MD (gt)
\(\widehat{EAM}=\widehat{FDM}\) (đã cm)
AE = DF (gt)
=> t/g AME = t/g DMF (c.g.c)
=> ME = MF (2 cạnh tương ứng)
=> M là trung điểm của EF
=> 3 điểm E, M, F thẳng hàng (áp dụng t/c mỗi đoạn thẳng chỉ có 1 trung điểm)
Xin lỗi, tối qua off sớm! Thu An giải bài 1;2;3;5 rùi, để t giải bài 4 vậy
4/ Hình, tự vẽ:
a/ Xét tam giác ABD và tam giác EBD có:
BE = BA (GT)
góc ABD = góc EBD (GT)
BD: cạnh chung
=> tam giác ABD = tam giác EBD (c.g.c)
Ta có: tam giác ABD = tam giác EBD
=> AD = ED (2 cạnh tương ứng)
b/ Ta có: tam giác ABD = tam giác EBD (ý a)
=> góc A = góc E = 900 (2 góc tương ứng)
Vậy DE vuông góc BC
Vì AH là đường cao của tam giác ABC
nên AH vuông góc BC
=> AH // DE (đpcm)
c/ Vì AH // DE (ý b)
=> góc AHM = góc MDK (so le trong) (1)
Ta có: DK = AH (GT) (2)
HM = MD (GT) (3)
Từ (1),(2),(3) => tam giác AHM = tam giác MDK
=> góc AMH = góc DMK (2 góc tương ứng)
Ta có: góc AMH + góc AMD = 1800 (kề bù)
=> góc DMK + góc AMD = 1800
=> góc AMK = 1800
hay A,M,K thẳng hàng
Bài 1:
a/ Trong t/g ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
hay \(90^o+53^o+\widehat{C}=180^o\)
=> \(\widehat{C}=180^o-90^o-53^o=37^o\)
b/ Xét t/g BEA và t/g BED có:
BE: Cạnh chung
\(\widehat{ABE}=\widehat{DBE}\left(gt\right)\)
BA = BD (gt)
=> t/g BEA = t/g BED (c.g.c)(đpcm)
c/ Xét t/g BHF và t/g BHC có:
\(\widehat{BHF}=\widehat{BHC}=90^o\)
BH : cạnh chung
\(\widehat{FBH}=\widehat{CDH}\left(gt\right)\)
=> t/g BHF = t/g BHC (g.c.g)(đpcm)
d/ Xét t/g BAC và t/g BDF có:
\(\widehat{BAC}=\widehat{BDF}=90^o\) (2 góc tương ứng do t/g BEA = t/g BED)
BA = BD (gt)
\(\widehat{B}:chung\)
=> t/g BAC = t/g BDF (đpcm)
Ta có: \(\widehat{DEB}+\widehat{BEF}=180^o\)
hay \(\widehat{DEF}=180^o\)
=> 3 điểm D, E, F thẳng hàng (đpcm)
Bài 5:
a/ Xét t/g ABD và t/g AED có:
AB = AE (gt)
\(\widehat{BAD}=\widehat{EAD}\left(gt\right)\)
AD: Cạnh chung
=> t/g ABD = t/g AED (c.g.c)
=> \(\widehat{ABD}=\widehat{AED}\) (2 góc tương ứng)
b/ Ta có:
\(\widehat{ABD}+\widehat{DBF}=180^o\) (kề bù)
\(\widehat{AED}+\widehat{DEC}=180^o\) (kề bù)
mà \(\widehat{ABD}=\widehat{AED}\) (ý a)
=> \(\widehat{DBF}=\widehat{DEC}\)
Xét t/g DBF và t/g DEC có:
\(\widehat{BDF}=\widehat{EDC}\) (đối đỉnh)
DB = DE (2 cạnh tương ứng do t/g ABD = t/g AED)
\(\widehat{DBF}=\widehat{DEC}\left(cmt\right)\)
=> t/g DBF = t/g DEC (g.c.g)
c/ Ta có: \(\widehat{ADC}+\widehat{CDN}=180^o\) (kề bù)
hay \(\widehat{ADN}=180^o\)
=> A,D,N thẳng hàng
mà AD // EM (gt)
=> DN // EM
Dễ thế! Tiếc là h mk bận luyện thi ioe cấp huyện rùi. Thu An giải hết vậy. Khi nào rảnh, khoảng mai hoặc chủ nhật mik ms có time để giải nhiều nhiều đc
các ban làm mấy câu khoanh tròn giúp mình với nhé mấy câu lũy thừa mình không hiểu lắm
