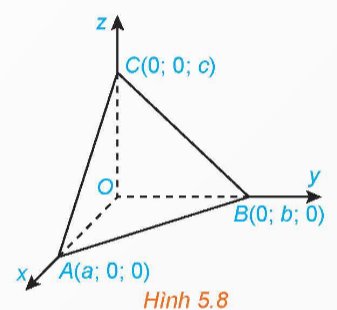
Mặt phẳng (ABC) có cặp vectơ chỉ phương \(\overrightarrow {AB} \left( { - a;b;0} \right),\overrightarrow {AC} \left( { - a;0;c} \right)\) nên có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
Ta có: \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}}b&0\\0&c\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - a}\\c&{ - a}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - a}&b\\{ - a}&0\end{array}} \right|} \right) = \left( {bc;ac;ab} \right)\)
Mặt phẳng (ABC) đi qua điểm A(a; 0; 0) và vectơ pháp tuyến \(\overrightarrow n = \left( {bc;ac;ab} \right)\) nên phương trình mặt phẳng (ABC) là:
\(bc\left( {x - a} \right) + acy + abz = 0 \Leftrightarrow bcx + acy + abz = bca \Leftrightarrow \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) (đpcm)