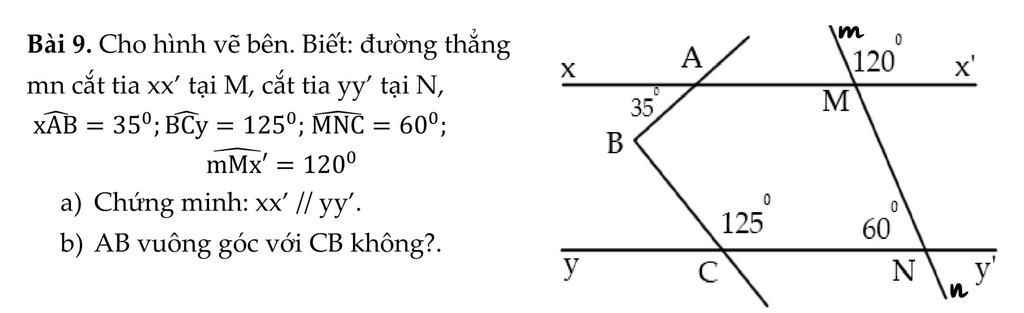Question

Giúpppppppppppppppppp

Answer 1

a, Ta có \(\widehat{mMx'}=\widehat{AMN}=120^0\left(đối.đỉnh\right)\)

\(\Rightarrow\widehat{AMN}+\widehat{MNC}=120^0+60^0=180^0\) mà 2 góc này ở vị trí trong cùng phía nên xx'//yy'

b, Kẻ Bz//xx'//yy'

Do đó \(\widehat{xAB}=\widehat{ABz}=35^0\) (so le trong) và \(\widehat{zBC}+\widehat{BCy'}=180^0\) (trong cùng phía)

\(\Rightarrow\widehat{zBC}=180^0-125^0=55^0\)

Do đó \(\widehat{ABC}=\widehat{zBA}+\widehat{zBC}=35^0+55^0=90^0\)

Vậy \(AB\perp BC\)

Answer 2

aVì N1 +N2=180*(kề bù )nên

N2=180*-N1

N2=180*-60*=120*

Vì M4=N2 ( đồng vị) =) xx'//yy'

b,Có