\(P\ge\dfrac{\left(x+y+z\right)^2}{\sqrt{15x^2+26xy+8y^2}+\sqrt{15y^2+26yz+8z^2}+\sqrt{15z^2+26zx+8x^2}}\)
\(\sqrt{15x^2+26xy+8y^2}=\sqrt{\left(5x+2y\right)\left(3x+4y\right)}\le\dfrac{\left(5x+2y+3x+4y\right)}{2}=\dfrac{8x+6y}{2}\)
\(tt\Rightarrow\sqrt{15y^2+26yz+8z^2}\le\dfrac{8y+6z}{2};\sqrt{15z^2+26zx+8x^2}\le\dfrac{8z+6x}{2}\)
\(\Rightarrow P\ge\dfrac{3^2}{\dfrac{8x+6y+8y+6z+8z+6x}{2}}=\dfrac{18}{14\left(x+y+z\right)}=\dfrac{18}{14.3}=\dfrac{3}{7}\)
\(dâu"="\Leftrightarrow x=y=z=1\)







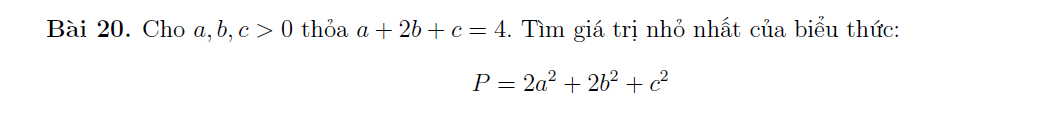

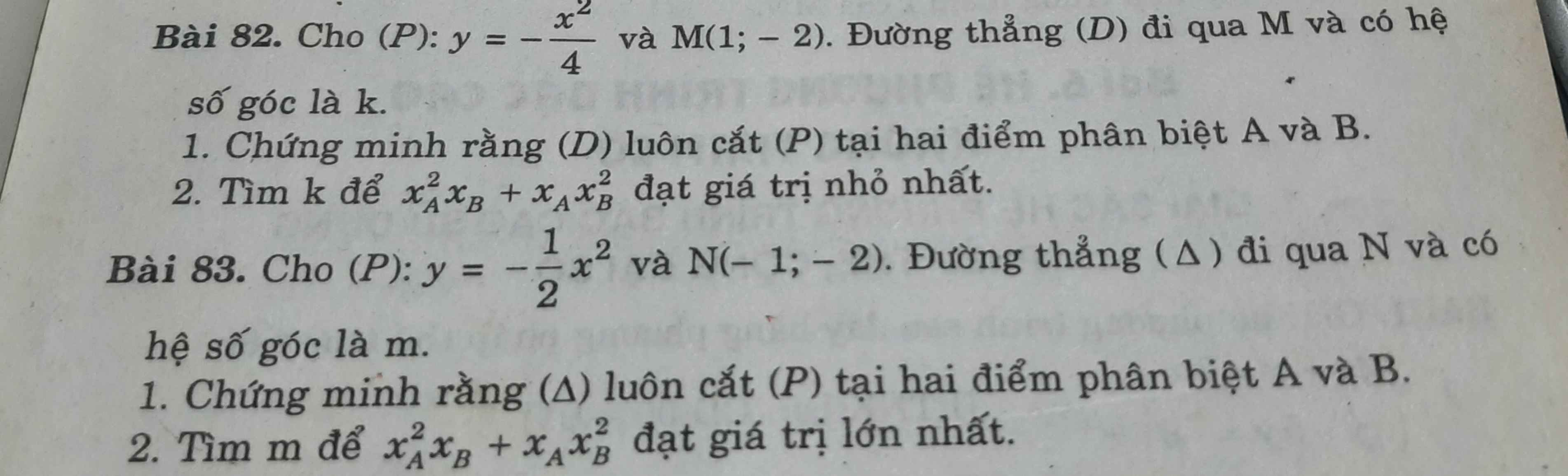








 Mọi người ơi,giúp em bài với ạ em cảm ơn ạ
Mọi người ơi,giúp em bài với ạ em cảm ơn ạ


