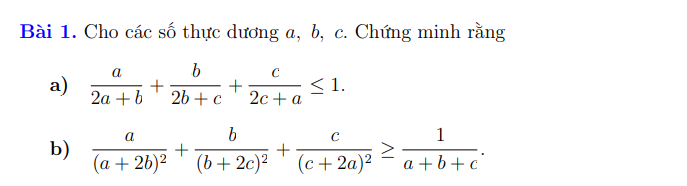4) a) Giả sử \(a\ge b\ge c\). Ta có
\(a< b+c\Leftrightarrow2a< a+b+c=2\Rightarrow a< 1\Rightarrow b< 1;c< 1\)
b) Từ câu a), ta suy ra: \(\left(1-a\right)\left(1-b\right)\left(1-c\right)>0\)
\(\Leftrightarrow ab+bc+bc>1+abc\)
Mặt khác, ta cũng có: \(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)\)
\(\Rightarrow4>a^2+b^2+c^2+2\left(1+abc\right)\)
\(\Rightarrow4>a^2+b^2+c^2+2+2abc\)
\(\Rightarrow2-2abc>a^2+b^2+c^2\Rightarrow a^2+b^2+c^2< 2\left(1-abc\right)\)





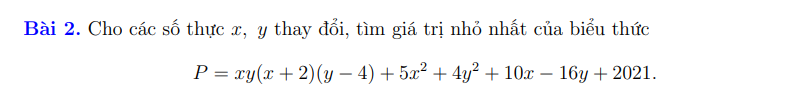









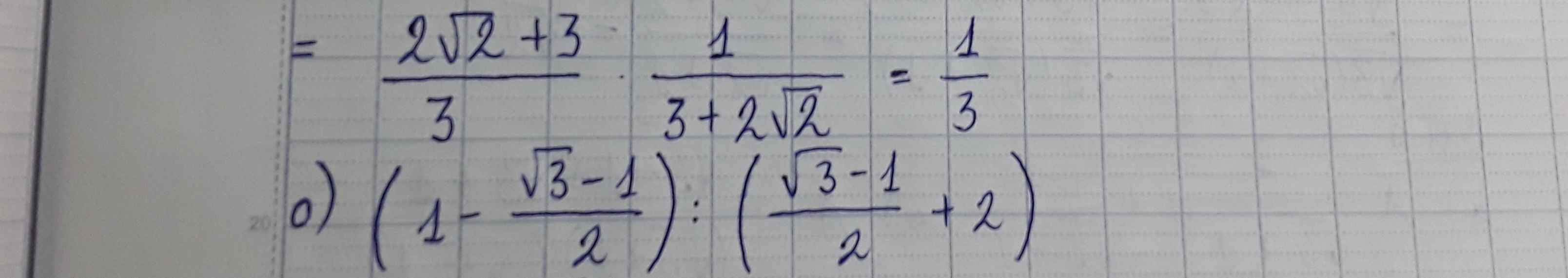 giải giúp mk câu o vs ạ
giải giúp mk câu o vs ạ