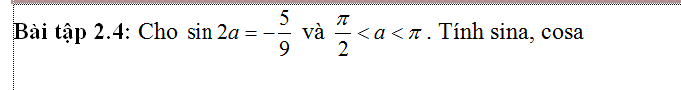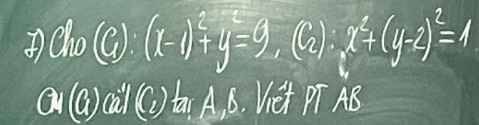\(\dfrac{\pi}{2}< a< \pi\Rightarrow\left\{{}\begin{matrix}sina>0\\cosa< 0\end{matrix}\right.\)
\(sin2a=-\dfrac{5}{9}\Leftrightarrow sina.cosa=-\dfrac{5}{18}\Rightarrow cosa=-\dfrac{5}{18sina}\)
Thế vào \(sin^2a+cos^2a=1\)
\(sin^2a+\dfrac{25}{324sin^2a}=1\Leftrightarrow sin^4a-sin^2a+\dfrac{25}{324}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2a=\dfrac{9-2\sqrt{14}}{8}\\sin^2a=\dfrac{9+2\sqrt{14}}{8}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sina=\sqrt{\dfrac{9-2\sqrt{14}}{8}};cosa=-\sqrt{\dfrac{9+2\sqrt{14}}{8}}\\sina=\sqrt{\dfrac{9+2\sqrt{14}}{8}};cosa=-\sqrt{\dfrac{9-2\sqrt{14}}{8}}\end{matrix}\right.\)