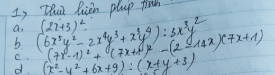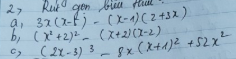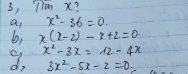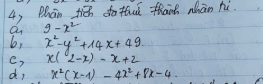Bài 1:
\(\dfrac{y-z}{\left(x-y\right)\left(x-z\right)}+\dfrac{z-x}{\left(y-z\right)\left(y-x\right)}+\dfrac{x-y}{\left(z-x\right)\left(z-y\right)}\)
\(=\dfrac{\left(x-z\right)-\left(x-y\right)}{\left(x-y\right)\left(x-z\right)}+\dfrac{\left(y-x\right)-\left(y-z\right)}{\left(y-z\right)\left(y-x\right)}+\dfrac{\left(z-y\right)-\left(z-x\right)}{\left(z-x\right)\left(z-y\right)}\)
\(=\dfrac{1}{x-y}-\dfrac{1}{x-z}+\dfrac{1}{y-z}-\dfrac{1}{y-x}+\dfrac{1}{z-x}-\dfrac{1}{z-y}\)
\(=\dfrac{1}{x-y}+\dfrac{1}{z-x}+\dfrac{1}{y-z}+\dfrac{1}{x-y}+\dfrac{1}{z-x}+\dfrac{1}{y-z}\)
\(=\dfrac{2}{x-y}+\dfrac{2}{z-x}+\dfrac{2}{y-z}\)
\(\Rightarrow\dfrac{y-z}{\left(x-y\right)\left(x-z\right)}+\dfrac{z-x}{\left(y-z\right)\left(y-x\right)}+\dfrac{x-y}{\left(z-x\right)\left(z-y\right)}=\dfrac{2}{x-y}+\dfrac{2}{y-z}+\dfrac{2}{z-x}\left(đpcm\right)\)
Vậy...
bài 1 b
Theo đề bài ta có :
S - P = \(\left(a^3_1+a^3_2+....+a^3_{2013}\right)-\left(a_1+a_2+....+a_{2013}\right)\)
= \(\left(a^3_1-a_1\right)+\left(a^3_2-a_2\right)+....\left(a^3_{2013}-a_{2013}\right)\)
= \(a_1\left(a^2_1-1\right)+a_2\left(a^2_2-1\right)+....a_{2013}\left(a^2_{2013}-1\right)\)
= \(a_1\left(a_1-1\right)\left(a_1+1\right)+a_2\left(a_2-1\right)\left(a_2+1\right)+....+a_{2013}\left(a_{2013}-1\right)\left(a_{2013}+1\right)\)
Dễ chứng minh \(a_1\left(a_1-1\right)\left(a_1+1\right)⋮6\) các số hạng còn lại cũng chứng minh tương tự
Suy ra S - P \(⋮\) 6
Nếu \(P⋮̸6\) thì \(S⋮̸6\) do đó \(S⋮6\) khi và chỉ khi P chia hết cho 6