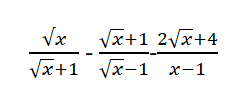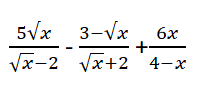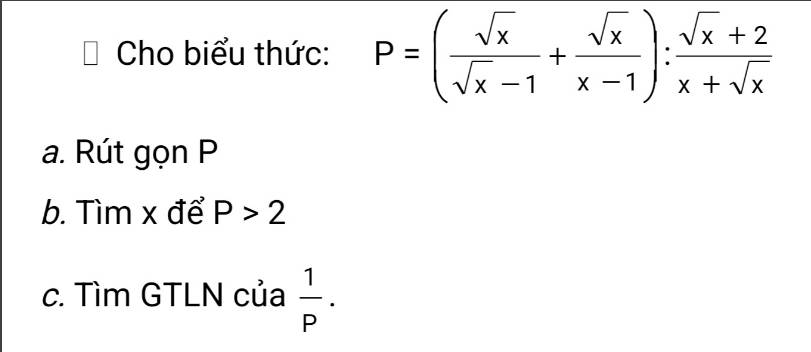a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne1\end{matrix}\right.\)
\(P=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{1-\sqrt{x}+x-\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
b: \(x=7-4\sqrt{3}=\left(2-\sqrt{3}\right)^2\)
Khi \(x=\left(2-\sqrt{3}\right)^2\) thì
\(P=\dfrac{2}{\left(2-\sqrt{3}\right)^2+\sqrt{\left(2-\sqrt{3}\right)^2}+1}\)
\(P=\dfrac{2}{7-4\sqrt{3}+2-\sqrt{3}+1}\)
\(=\dfrac{2}{10-5\sqrt{3}}=\dfrac{4+2\sqrt{3}}{5}\)
c: P>=2/3
=>P-2/3>=0
=>\(\dfrac{2}{x+\sqrt{x}+1}-\dfrac{2}{3}>=0\)
=>\(\dfrac{1}{x+\sqrt{x}+1}-\dfrac{1}{3}>=0\)
=>\(\dfrac{3-x-\sqrt{x}-1}{3\left(x+\sqrt{x}+1\right)}>=0\)
=>\(-x-\sqrt{x}+2>=0\)
=>\(x+\sqrt{x}-2< =0\)
=>\(\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)< =0\)
=>\(\sqrt{x}-1< =0\)
=>0<=x<=1
Kết hợp ĐKXĐ, ta được: 0<=x<1
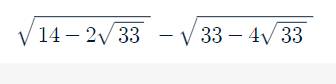Cíu mình dới mn ơi huhu
giúp em vs gấp quá
