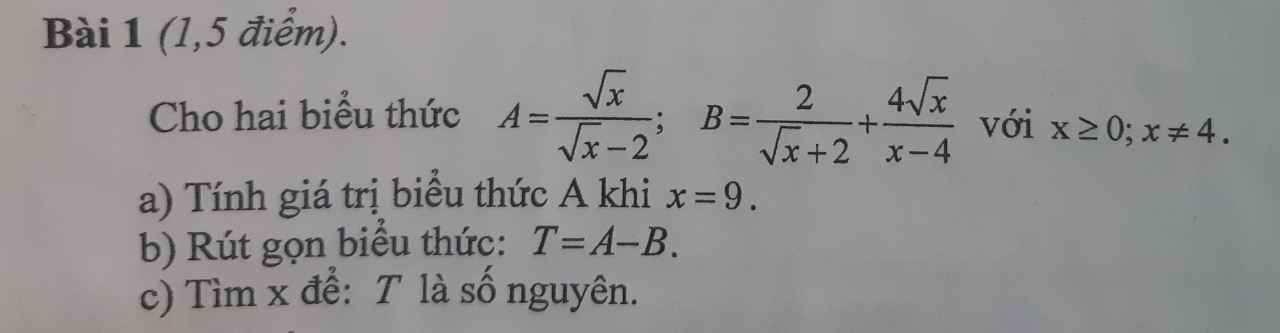câu a
Khi x=0 thì A=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}\)=\(\dfrac{\sqrt{9}}{\sqrt{9}-2}\) =\(3\)
câu b
Đk:x\(\ge0,x\ne4\)
\(A-B\)=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\left(\dfrac{2}{\sqrt{x}+2}+\dfrac{4\sqrt{x}}{x-4}\right)\)
=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2\left(\sqrt{x}-2\right)+4\sqrt{x}}{x-4}\)
=\(\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)-2\left(\sqrt{x}-2\right)-4\sqrt{x}}{x-4}\)
=\(\dfrac{x+2\sqrt{x}-2\sqrt{x}+4-4\sqrt{x}}{x-4}\)
=\(\dfrac{x-4\sqrt{x}+4}{x-4}\) =\(\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
câu c
T=\(\dfrac{\sqrt{x}-2}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2-4}{\sqrt{x}+2}\)=\(1-\dfrac{4}{\sqrt{x}+2}\)
Để T nguyên thì 4\(⋮\) \(\sqrt{x}+2\) \(\Leftrightarrow\) \(\sqrt{x}+2\inƯ\left(4\right)\)
\(\Rightarrow\)\(x\in\left\{0;4\right\}\) thì T nguyên
a) Thay x=9 vào A, ta được:
\(A=\dfrac{3}{3-2}=3\)
b) Ta có: T=A-B
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}+2}-\dfrac{4\sqrt{x}}{x-4}\)
\(=\dfrac{x+2\sqrt{x}-2\sqrt{x}+4-4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)