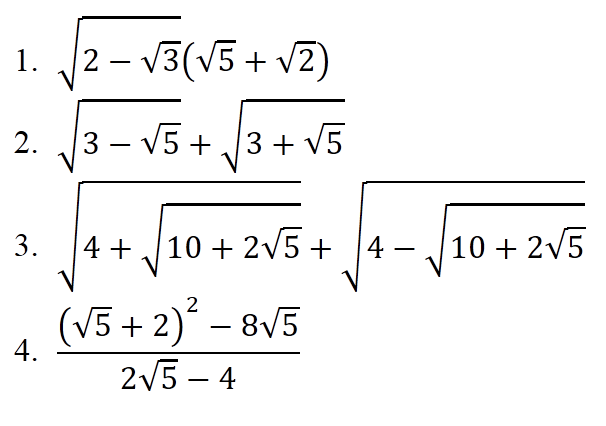Question

Giúp mình phần b với ạ, mình cảm ơn nhiềuuu

Answer 1

Thay m=2 vào HPT ta có: 

\(\left\{{}\begin{matrix}2x+y=1\\x+2y=1\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}4x+2y=2\\x+2y=1\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}4x+2y=2\\3x=1\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)

Answer 2

b) \(\left\{{}\begin{matrix}mx+y=1\\x+my=1\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}y=1-mx\\x+m\left(1-mx\right)=1\left(1\right)\end{matrix}\right.\)

(1) ⇔x+m-m²x=1

⇔x(1-m²)=1-m (2)

TH1: 1-m² = 0

⇔m = +- 1

Thay m=1 vào (2) ta có: 0x=0 (Luôn đúng) ⇒m=1 (chọn)

Thay m=-1 vào (2) ta có: 0x=2 (Vô lí) ⇒m=-1 (loại)

TH2: 1-m² ≠0

⇔m≠ +-1

⇒HPT có nghiệm duy nhất:

x=  \(\dfrac{1-m}{1-m^2}\)

⇒y= \(1-m.\dfrac{1-m}{1-m^2}\)

⇔y=\(\dfrac{1-m}{1-m^2}\)

Dễ thấy x=y nên: 

\(\dfrac{1-m}{1-m^2}>0\)

⇔1-m>0

⇔m<1

Vậy m <1 thì Thỏa mãn yêu cầu đề bài.

 

 

 

Answer 3

a) Thay m=2 vào hệ phương trình, ta được:

\(\left\{{}\begin{matrix}2x+y=1\\x+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=1\\2x+4y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-3y=-1\\2x+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{3}\\2x=1-y=\dfrac{2}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)

Vậy: Khi m=2 thì hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)