\(=\left[{}\begin{matrix}\dfrac{5}{8}-x+\dfrac{1}{4}-\dfrac{3}{2}\\x-\dfrac{5}{8}+\dfrac{1}{4}-\dfrac{3}{2}\end{matrix}\right.=\left[{}\begin{matrix}-x-\dfrac{5}{8}\\x-\dfrac{15}{8}\end{matrix}\right.\)
\(2.\left|\dfrac{5}{8}-x\right|=\dfrac{5}{4}\\\left|\dfrac{5}{8}-x\right|=\dfrac{5}{8} \\ \left[{}\begin{matrix}\dfrac{5}{8}-x=\dfrac{5}{8}\\\dfrac{5}{8}-x=-\dfrac{5}{8}\end{matrix}\right.\left[{}\begin{matrix}x=0\\x=\dfrac{5}{4}\end{matrix}\right.\)
\(|\dfrac{5}{8}-x|+\dfrac{1}{4}=\dfrac{3}{2}\)
\(|\dfrac{5}{8}-x|=\dfrac{3}{2}-\dfrac{1}{4}\)
\(|\dfrac{5}{8}-x|=\dfrac{5}{4}\)
\(\Rightarrow\dfrac{5}{8}-x=\pm\dfrac{5}{4}\)
\(\dfrac{5}{8}-x=\dfrac{5}{4}\) \(\dfrac{5}{8}-x=-\dfrac{5}{4}\)
\(x=\dfrac{5}{8}-\dfrac{5}{4}\) \(x=\dfrac{5}{8}+\dfrac{5}{4}\)
\(x=-\dfrac{5}{8}\) \(x=\dfrac{15}{8}\)
\(\Rightarrow x=\left\{-\dfrac{5}{8};\dfrac{15}{8}\right\}\)




















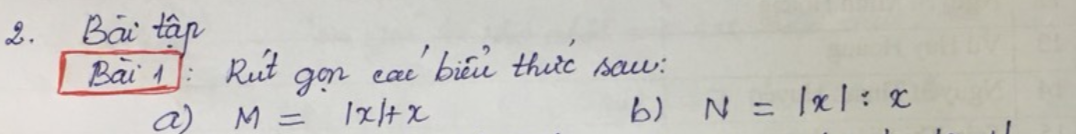 giúp mình câu này nhanh với ạ
giúp mình câu này nhanh với ạ