4: \(x^4-2x^2+1=\left(x^2-1\right)^2=\left(x-1\right)^2\cdot\left(x+1\right)^2\)
13: \(x^2-8x+7=\left(x-7\right)\left(x-1\right)\)
14: \(2x^2-5x+2=\left(x-2\right)\left(2x-1\right)\)
13: Ta có: \(x^2-8x+7\)
\(=x^2-x-7x+7\)
\(=\left(x-1\right)\left(x-7\right)\)
14: Ta có: \(2x^2-5x+2\)
\(=2x^2-4x-x+2\)
\(=\left(x-2\right)\left(2x-1\right)\)
20: Ta có: \(x^3-5x^2+8x-4\)
\(=x^3-2x^2-3x^2+6x+2x-4\)
\(=\left(x-2\right)\left(x^2-3x+2\right)\)
\(=\left(x-2\right)^2\cdot\left(x-1\right)\)

 giúp mình được ko
giúp mình được ko 








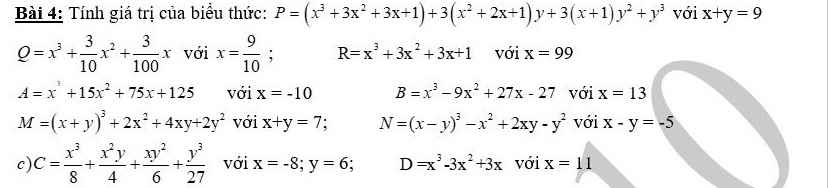
 giúp mình bài 4 câu B,C D với ạ
giúp mình bài 4 câu B,C D với ạ



