Điều kiện xác định: \(x\ge3\)
\(3\sqrt{9x-27}-\dfrac{2}{5}\sqrt{25x-75}=\dfrac{1}{2}\sqrt{4x-12}\)
\(\Leftrightarrow3\sqrt{9\left(x-3\right)}-\dfrac{2}{5}\sqrt{25\left(x-3\right)}=\dfrac{1}{2}\sqrt{4\left(x-3\right)}\)
\(\Leftrightarrow3.3\sqrt{x-3}-\dfrac{2}{5}.5\sqrt{x-3}=\dfrac{1}{2}.2\sqrt{x-3}\)
\(\Leftrightarrow9\sqrt{x-3}-2\sqrt{x-3}=\sqrt{x-3}\)
\(\Leftrightarrow6\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\) (thỏa mãn)
Vậy phương trình có tập nghiệm là: \(S=\left\{3\right\}.\)
\(\Leftrightarrow9\sqrt{x-3}-2\sqrt{x-3}=\sqrt{x-3}+15\)
=>6 căn x-3=15
=>căn x-3=2,5
=>x-3=6,25
=>x=9,25








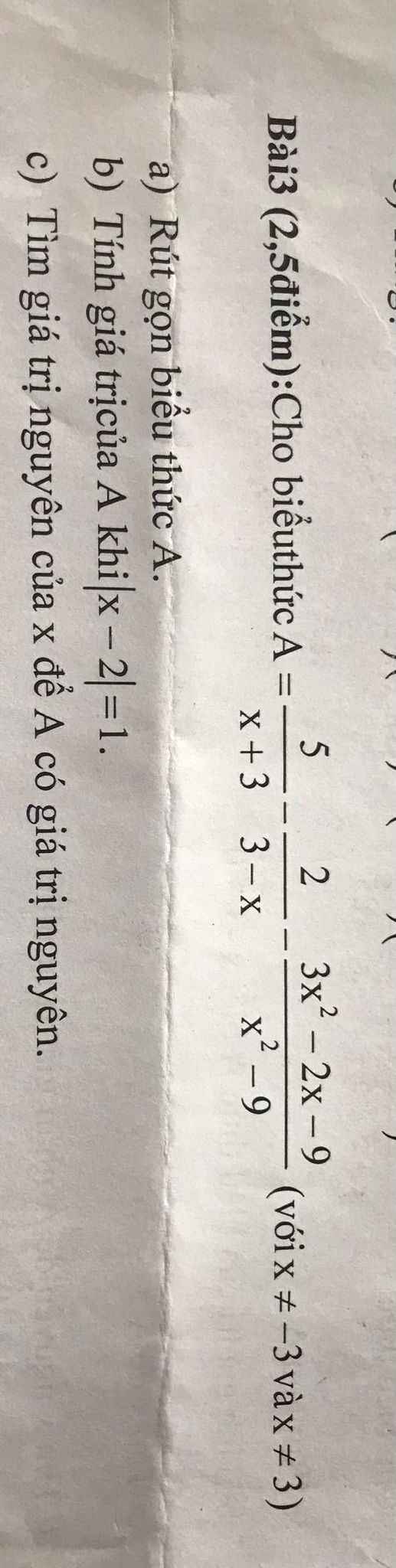



 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)







