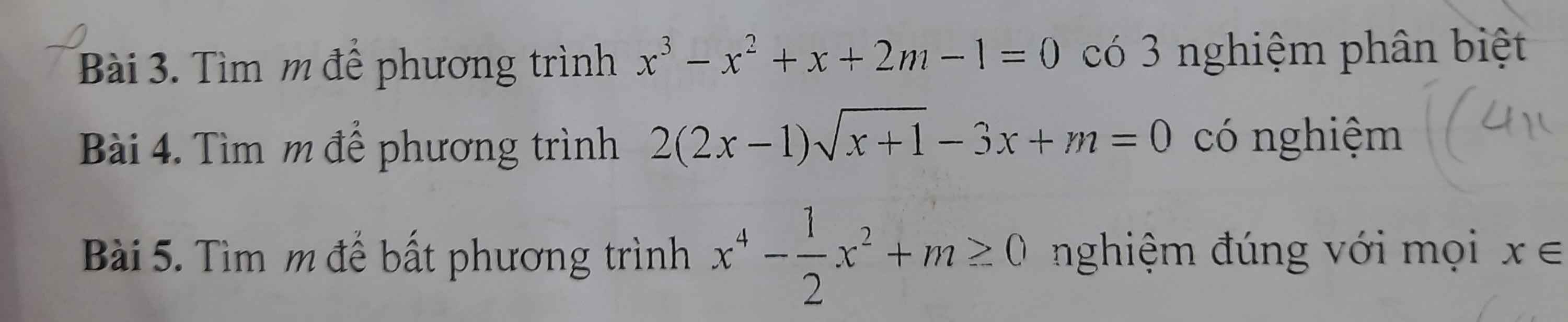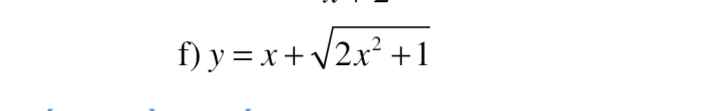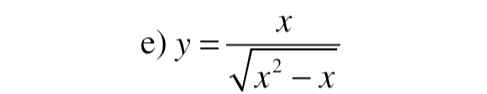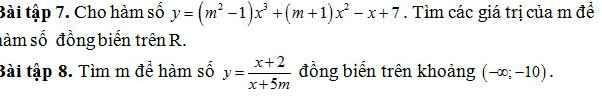\(x\ge-1\)
Đặt \(t=\sqrt{x+1},t\ge0\Rightarrow t^2-1=x\)
(NX: 1t chỉ có 1x)
Pttt:\(2\left(2t^2-2-1\right)t-3\left(t^2-1\right)+m=0\)
\(\Leftrightarrow4t^3-3t^2-6t+3=-m\) (*)
Xét\(f\left(t\right)=4t^3-3t^2-6t+3,t\ge0\)
\(f'\left(t\right)=12t^2-6t-6\)
\(f'\left(t\right)=0\Leftrightarrow t=1\)
BBT:
\(t\) \(0\) \(1\) \(+\infty\)
\(f'\left(t\right)\) || \(-\) \(0\) \(+\)
\(f\left(t\right)\) \(3\) \(-2\)
Số gđ của đồ thị \(f\left(t\right)\) và đường thẳng \(d=-m\) là số nghiệm của pt (*)
Để pt ban đầu có nghiệm khi pt (*) có nghiệm
\(\Leftrightarrow-m\ge-2\)
\(\Leftrightarrow m\le2\)
Vậy ...