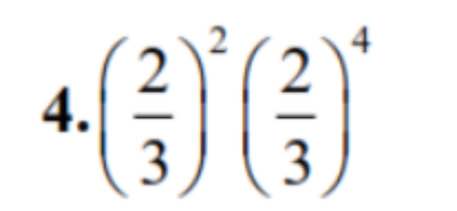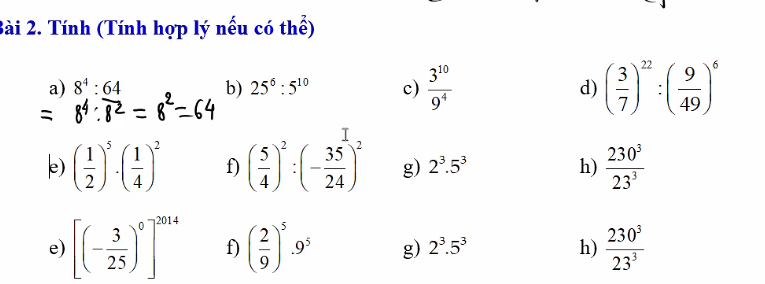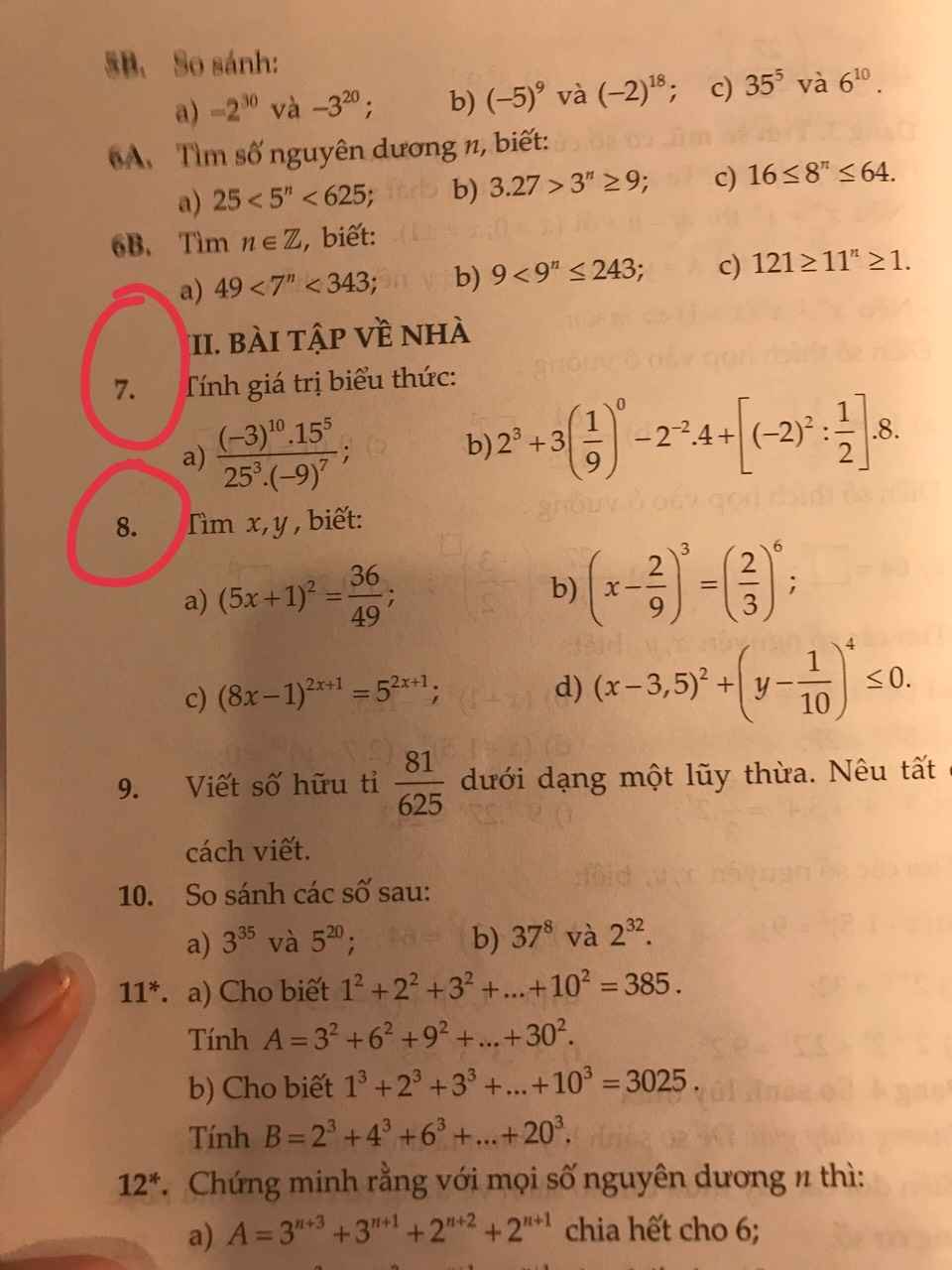\(a,=\dfrac{1}{64}\cdot64=1\\ b,=\left(\dfrac{3}{4}\cdot\dfrac{4}{3}\right)^3+\dfrac{1}{3}=1+\dfrac{1}{3}=\dfrac{4}{3}\\ c,=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\\ d,=\dfrac{1}{2^{2004}}\cdot9^{1002}\\ =\dfrac{9^{1002}}{4^{1002}}=\left(\dfrac{3}{2}\right)^{1002}\)
a. (0,125)2 . 64
= \(\dfrac{1}{64}.\dfrac{64}{1}\)
= \(\dfrac{1.1}{1.1}=1\)